АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос 43. Медиана распределения случайной величины

Читайте также:
  1. I. Постановка вопроса
  2. IХ. Примерный перечень вопросов к итоговой аттестации
  3. Авторская статья Владимира Путина «Россия: национальный вопрос» (выдержки)
  4. АК. Структура белков, физико-химические свойства (192 вопроса)
  5. Аксиома вторая. Вопрос о производственных отношениях вторичен по отношению к вопросу о типе жизнедеятельности.
  6. Альтернативный вопрос (вопрос выбора)
  7. Анализ состояния вопроса
  8. Анамнез и его разделы. Приоритет отечественной медицины в разработке анамнестического метода. Понятие о наводящих вопросах: прямых и косвенных.
  9. Биноминальная случайная величина, ее мат. ожидание и дисперсия. Случаи применения этой случайной величины.
  10. БЛОК № 3 (вопрос 9 – нет ответа)
  11. В 4. Виды производственного освещения и их характеристика. Основные светотехнические величины и единицы их измерения, КЕО.
  12. В 4. Виды производственного освещения и их характеристика. Основные светотехнические величины и единицы их измерения. КЕО

Медиана - это значение признака, которое делит всю выборку на две равные части. Половина вариант имеют значения меньшие, чем медиана, а половина - большие. Проще всего значение медианы определяется в случае несгруппированного набора данных. Для того, чтобы определить медиану, надо предварительно упорядочить все элементы выборки по возрастанию (ранжировать). В том случае, если число элементов в выборке нечётное, медиана будет равна варианте, имеющей в ранжированном ряду порядковый номер:

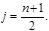То есть где Действительно, так как число элементов в выборке нечётное, величина j будет целой, причём как слева от x j, так и справа в ранжированном ряду будет находится по (n-1)/2 элементов, то есть x j делит выборку на две группы с одинаковым числом наблюдений. В том случае, если выборка будет иметь чётное число наблюдений, медиана будет находится по середине между n/2-м и n/2+1-м наблюдением. То есть: где 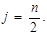В том случае, если медиану надо определить для сгруппированного набора данных, сначала определяют в каком классе она находится. Проще всего это сделать, если имеются в наличии накопленные частоты вариационного ряда. Класс, в котором находится медиана (медианный класс) это первый класс у которого накопленная частота окажется больше, чем n/2. В случае дискретной вариации, когда данные группировались в безинтервальный вариационный ряд, значение этого класса и будет медианой. Если группировка производилась в интервальный вариационный ряд, то предполагая, что внутри медианного интервала наблюдения располагаются равномерно, медиану можно определить по формуле:

, где 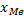- центр медианного ряда; λ- величина интервала; n - объём выборки; j - номер медианного интервала; - накопленная частота предшествующего ряда медианному класса; 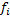- частота медианного класса.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)