 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Код Шенонна-Фано
Лабораторна робота №9
Приклад 1 Нехай джерело видає одне з 8 повідомлень А...З, що мають однакову імовірність.
Кодування цих повідомлень рівномірним трирозрядним кодом наведено в табл. 2.1. Тоді:
- ентропія джерела  (біт/сим);
(біт/сим);
- надлишковість джерела  ;
;
- середня довжина коду 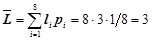 (біт/сим);
(біт/сим);
- надлишковість коду  .
.
Отже, при передачі рівноімовірних повідомлень надлишковість рівномірного коду дорівнює нулю, тобто в цьому випадку рівномірне кодування є оптимальним.
Приклад 2 Припустимо, що повідомлення нерівноймовірні (табл. 2.2).
Таблиця 2.2
| А | Б | В | Г | Д | Е | Ж | З |
| 0,6 | 0,2 | 0,1 | 0,04 | 0,025 | 0,015 | 0,01 | 0,01 |
Ентропія джерела при цьому буде менше: Н(Х)» 1,781 (біт/сим).
Середнє число символів на одне повідомлення при використовуванні рівномірного трирозрядного коду  (біт/сим).
(біт/сим).
Надлишковість коду  , тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).
, тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).
Отже, при кодуванні нерівноімовірних повідомлень рівномірні коди характеризуються значною надмірністю. У таких випадках доцільно використовувати нерівномірні коди, довжина кодових комбінацій яких залежить від імовірності символів в повідомленні. Таке кодування називається статистичним. Нерівномірний код при статистичному кодуванні вибирається так, щоб більш імовірні значення передавалися за допомогою більш коротких комбінацій коду, а менш імовірні - за допомогою більш довгих. У результаті зменшується середня довжина коду.


Приклад 3. Задано 8 повідомлень та ймовірності їх появи. Побудувати код Шеннона-Фано.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
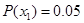 ,
,  .
.
Код Шеннона-Фано:
Для побудови коду Шеннона-Фано всі повідомлення  записуються в порядку спадання їх ймовірностей.
записуються в порядку спадання їх ймовірностей.

| 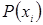
| Поділ повідомлення на підгрупи | Код | 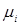
| 
| |||

| 0.27 | 0.54 | ||||||

| 0.23 | 0.46 | ||||||

| 0.14 | 0.42 | ||||||
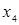
| 0.12 | 0.36 | ||||||

| 0.07 | 0.28 | ||||||
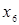
| 0.06 | 0.24 | ||||||

| 0.06 | 0.24 | ||||||

| 0.05 | 0.20 |
Записані таким чином повідомлення розбиваються на дві по можливості рівноймовірні підгрупи. Всім повідомленням першої підгрупи присвоюють 1 в якості кодового символу, а всім повідомленням другої підгрупи – 0. Аналогічне ділення на підгрупи робиться до тих пір, доки в кожну підгрупу не попаде одне повідомлення. Знайдений код по Шеннону-Фано дуже близький до оптимального. Щоб це перевірити, знайдемо ентропію цих повідомлень:


 .
.
Визначимо середню довжину кодового слова:
 .
.
Знайдемо середне число нулів:
 .
.
Знайдемо середне число одиниць:
 .
.
Перевірка: 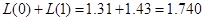 .
.
Ймовірність появи нулів:  .
.
Ймовірність появи одиниць:  .
.
Перевірка:  .
.
Так як  , то говорять, що поява символів є рівноймовірна, а тому отриманий код є близьким до оптимального.
, то говорять, що поява символів є рівноймовірна, а тому отриманий код є близьким до оптимального.
Приклад 4. Для ансамблю повідомлень, заданого таким розподілом ймовірностей: 0,18; 0,17; 0,16; 0,15; 0,1; 0,08; 0,05; 0,05; 0,04; 0,02, побудувати двійкові коди Шеннона-Фано і Хаффмена. Визначити основні характеристики кодів.
Розв'язання
Верхня границя компактності кодування повідомлень дискретної випадкової величини (д. в. в.) визначається її ентропією
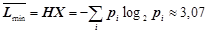 (біт/сим).
(біт/сим).
Обчислимо середню довжину оптимальних кодів Шеннона-Фано і Хаффмена для кодування даної д. в. в.
I Метод Шеннона-Фано:
Побудуємо таблицю кодів Шеннона-Фано (табл. 1):
Таблиця 1
| Імовірність pi | Код Code (xi) | Довжина коду li | pili |
| 0,18 | 0,36 | ||
| 0,17 | 0,51 | ||
| 0,16 | 0,48 | ||
| 0,15 | 0,45 | ||
| 0,1 | 0,3 | ||
| 0,08 | 0,32 | ||
| 0,05 | 0,2 | ||
| 0,05 | 0,2 | ||
| 0,04 | 0,2 | ||
| 0,02 | 0,1 | ||
| S pili = 3,12 |
Середня довжина даного коду: 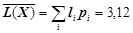 (біт/сим).
(біт/сим).
Отже, ефективність коду  ,
,
надлишковість коду  .
.
Поиск по сайту: