 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи для самостоятельного решения. К практическим занятиям
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К практическим занятиям
По курсу «Математика. Раздел: Теория вероятностей, математическая статистика и случайные процессы»
Выпуск 10.
Тема 10: Проверка статистических гипотез.
Для решения задач по данной теме необходимо освоить теоретический материал в соответствии с программой курса: раздел 4.2, подразделы 1 и 2. Для этого необходимо изучить разделы учебных пособий: [3], глава 4, [6],глава 11, [8],глава 10, [9],глава 4.4.
1. Решение типовой задачи. Рассмотрим задачу 5.
Введем обозначения: Значение параметра в основной гипотезе m 0 = 40 мм, значение параметра в конкурирующей. гипотезе m 1 = 43 мм, граница критической области с = 40,1 мм, объем выборки n = 36, дисперсия s2 = 1 мм2, ошибка первого рода a, ошибка второго рода b.
Граничное значение критерия: 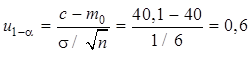 .Расстояние между гипотезами
.Расстояние между гипотезами  .
.
Ошибка первого рода 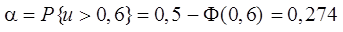 .
.
Ошибка второго рода при односторонней гипотезе:
 .
.
Задачи для самостоятельного решения.
Задача 1. Давление в камере контролируется по двум манометрам. Для сравнения точности приборов одновременно фиксируются их показания. По результатам 10 замеров выборочные средние составили 15,3 и 16,1; выборочные дисперсии соответственно 0,2 и 0,15. Используя двусторонний и односторонний критерии, проверить с уровнем значимости 0,1: а) гипотезу о равенстве дисперсий, б) гипотезу о равенстве средних.
Задача 2. Автомат обрабатывает болты с номинальным значением контролируемого размера 40 мм. Полагая, что распределение нормальное с дисперсией 1 мм2 и что партия бракуется, если выборочное среднее больше 40,1 мм, найти вероятности ошибок первого и второго рода при альтернативной гипотезе Н1: среднее значение равно 40,3 мм. Решение принимается по выборке объема 36.
Задача 3. Автомат обрабатывает болты с номинальным значением контролируемого размера 40 мм. Полагая, что распределение нормальное с дисперсией 1 мм2 и что партия бракуется, если выборочное среднее больше 40,2 мм, найти вероятности ошибок первого и второго рода при альтернативной гипотезе Н1: среднее значение равно 40,3 мм. Решение принимается по выборке объема 36.
Задача 4. Технологический участок производства некоторого вещества дает в среднем 1000 кг продукции в сутки при с.к.о. среднего значения 80 кг. После внедрения новой технологии среднее значение за тот же период осреднения увеличилось до 1200 кг/сутки при том же с.к.о. Считая эту гипотезу альтернативной основной гипотезе о том, что производительность не изменилась, принять решение о справедливости гипотезы и найти мощность критерия, если уровень значимости равен: а)0,05, б)0,10. Принять решение также для альтернативной гипотезы Н1: производительность 1100 кг/сутки.
Задача 5. Из продукции автомата, обрабатывающего болты с номинальным значением параметра 40 мм, взята выборка объема 36. Выборочное среднее 40,2 мм. Дисперсия известна и равна 1 мм2. Можно ли по результатам этого обследования утверждать, что параметр не имеет положительного смещения относительно номинального значения? Определить критическую область для уровня значимости 0,01.
Задача 6. Из продукции автомата, обрабатывающего болты с номинальным значением параметра 40 мм, взята выборка для контроля качества. Дисперсия известна и равна 1 мм2. Какой минимальный объем выборки может обеспечить ошибки первого и второго рода не более 0,1 при альтернативной гипотезе: значение параметра 40,3 мм? Какая критическая область соответствует этим условиям?
Задача 7. Определить объем однократной выборки в биномиальном плане контроля надежности, проводимого в интересах заказчика, который требуется для браковки партии изделий с вероятностью безотказной работы не более 0,85, если браковочное число взято равным 1, а риск заказчика 0,1. Сделать то же самое при браковочном числе 2 и риске 0,05.
Задача 8. Новый метод измерения длины деталей был апробирован на эталоне и было установлено, что дисперсия результатов измерения по 10 замерам составляет 100 мкм2. Согласуется ли это результат с утверждением, что дисперсия не превосходит 50 мкм2? Уровень значимости принять равным 0,05.
Задача 9. Проверить гипотезу о том, что параметр экспоненциального распределения равен 0,001 ч-1, если известно, что при испытаниях 100 изделий получено 100 значений случайной величины и эмпирическое среднее 1100 час. Уровень значимости взять 5%.
Задача 10. Ожидается, что добавление специальных веществ уменьшает жесткость воды. Оценки жесткости воды до и после добавления специальных веществ по 40 и 50 пробам соответственно показали средние значения 4,0о и 3,8о жесткости. Дисперсия измерений в обоих случаях предполагается равной 0,25 градуса. Подтверждают ли эти результаты ожидаемый дефект? Принять уровень значимости равным 0,05.
Задача 11. Проверить гипотезу статистической значимости расхождения эмпирических средних для наработки до отказа в двух выборках: 2000 час и 2100 час. Уровень значимости равен 0,1. Размеры выборок: 80 и 120 соответственно. Наработка имеет нормальное распределение с одинаковыми дисперсиями для обеих выборок, равными 140000 час2.
Задача 12. При применении определенной процедуры проверки коэффициента трения шины автомобиля по мокрому асфальту установлено, что дисперсия результатов измерений этого коэффициента составляет 0,1. Несмещенная выборочная дисперсия, вычисленная по результатам 25 измерений коэффициента трения, оказалась равной 0,2. Используя двусторонний критерий, проверить гипотезу о том, что дисперсия результатов измерений равна 0,1 при уровне значимости 0,1. Решить эту же задачу другим способом, используя метод доверительных интервалов.
Задача 13. При исследовании влияния двух типов покрытий на удельную проводимость телевизионных трубок получены результаты (в условных единицах), приведенные в таблице
| № | Sхi | Sхi2 | ||||||
| 1 тип | - | |||||||
| 2 тип |
Можно ли по этим данным считать, что тип покрытия влияет на удельную проводимость трубок? Уровень значимости взять равным 0,10.
Задача 14. Для выпуска однородной продукции надо подобрать два станка. С этой целью в цехе установили три станка А, В и С и изготовили на них соответственно 16, 25 и 13 деталей. Выборочные значения средних и дисперсии на них оказались равными (37,5 мм; 36,8 мм; 38,3 мм), (1,21 мм2, 1,44 мм2, 3,08 мм2). Используя двусторонний критерий, проверить гипотезу о том, что какие-либо два станка дают одинаковые значения контролируемого параметра. Уровень значимости принять равным 0,10.
Задача 15. Составить план контроля вероятности отказа: а) в интересах изготовителя, б) в интересах заказчика. Риск изготовителя и заказчика взять равным 10%. Продукция считается кондиционной, если вероятность отказа не более 0,01, и некондиционной, если она более 0,2.
Задача 16. Составить план последовательного контроля надежности невосстанавливаемых изделий по вероятности безотказной работы (ВБР), принимая риски изготовителя и заказчика равными 10%. Рассчитать план в табличной форме до 10 отказов. Продукция считается кондиционной, если ВБР не менее 0,95, и некондиционной, если ВБР менее 0,8.
Задача 17. Построить план последовательного контроля вероятности безотказной работы (ВБР) невосстанавливаемых изделий, для которых надежность считается приемлемой, если ВБР не менее 0,99, и неприемлемой, если ВБР менее 0,9. Контроль осуществляется с риском заказчика не более 4% и риском поставщика не более 8%. Принять решение для случаев: (число изделий, число отказов) = (35, 1), (50, 2), (80, 2).
Задача 18. Построить план последовательного контроля вероятности безотказной работы (ВБР) невосстанавливаемых изделий, для которых надежность считается приемлемой, если ВБР не менее 0,99, и неприемлемой, если ВБР менее 0,8. Контроль осуществляется с риском заказчика и поставщика не более 10%. Сравнить с планом контроля по однократной выборке: а) в интересах изготовителя, б) в интересах заказчика. Составить критерий усеченного последовательного контроля.
Поиск по сайту: