 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение задачи в MS Excel
Практическая работа.
Решение уравнений методом половинного деления в MS Excel.
Цель работы: сформировать представления о численных методах решения уравнений, умения решать практические задачи методом половинного деления в MS Excel, проверить знания различных способов адресации в MS Excel, особенности использования условной функции.
 |
Задача. Решите уравнение (x-2)(x-9)=0 методом половинного деления. Прежде всего, следует отметить, что уравнение имеет два корня: х=2, х=9.
Решение задачи в MS Excel.
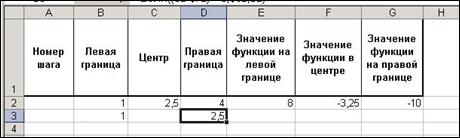
1. Заполните первую строку (шапку) таблицы в соответствии с рис. 1.
 |
2. Заполните вторую сроку таблицы. Для этого в ячейку B2 введите число 1 - это начальное значение для левой границы диапазона, на котором будет осуществляться поиск решения. Соответственно, в ячейку D2 введите в качестве значения правой границы диапазона, например, число 4. В столбце C будут отображаться центральные точки диапазона. поэтому, в ячейку C2 введите формулу =(B2+D2)/2. Теперь в ячейку E2 введите формулу =(B2-2)*(B2-9). После этого следует скопировать данную формулу в ячейку F2 и затем в ячейку G2. В результате в ячейке E2 будет определяться значение функции на левой границе диапазона, в ячейке F2 будет отображено значение в центре диапазона, и, наконец, в ячейке G2 — на правой границе диапазона. Проверьте правильность выполнения этапа по рис. 1.
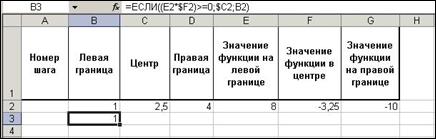 |
Рис. 1.
3. Заполните третью строку таблицы (рис. 2). В эту строку заносим данные, которые будут отображать состояние процесса поиска решения на первом шаге. Так, в ячейку B3 вводим формулу =если((E2*$F2)>=0;$C2;B2). Числовое значение будет присвоено этой ячейке после проверки условия E2*$F2>=0. Другими словами, проверяется знак произведения значения функции на левой границе диапазона и в средней точке. Если оно неотрицательно (а это значит, что оба значения одного знака или одно из них нуль), то левой границей становится средняя точка интервала. В противном случае левая граница интервала не меняется.
Рис. 2.
Теперь копируем формулу из ячейки B3 в ячейку DЗ, в ячейку CЗ копируем формулу из ячейки C2 (см. рис. 3).
Рис. 3.
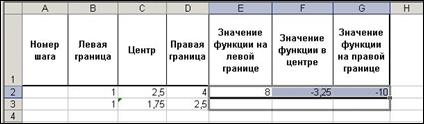
Далее с помощью маркера заполнения скопируйте формулы из диапазона E2:G2 в диапазон E3:G3. (рис. 4).
Рис. 4.
 |
4. Найдем первый корень уравнения. Для этого выделите диапазон A3:F3 и маркером заполнения захватите 16 строк вниз (рис. 5). В результате такой операции в нижней строке будут отображены данные, относящиеся к очередному итерационному шагу по сужению интервала, содержащего корень уравнения. Этот процесс можно продолжать до тех пор, пока решение не будет найдено с нужной точностью.
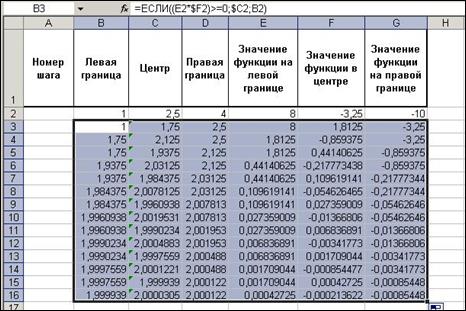 |
Рис. 5.
Контрольные вопросы и задания.
1. Почему в формуле для ячейки B3 указано нестрогое равенство нулю? Предположите, как изменится корень уравнения, если указать в этой ячейке строгое равенство?
2. Для чего в решении задачи использована условная функция?
3. Почему в записи условной функции указаны смешанные ссылки?
4. Какова станет запись формулы в ячейке D3 после копирования в нее условной функции из ячейки B3?
5. Каков первый корень уравнения? Какова при этом корне точность решения?
6. Определите корень уравнения с точностью до 10-3.
7. Найдите второй корень уравнения с точностью 10-4.
8. Найдите корни уравнения с заданной точностью:
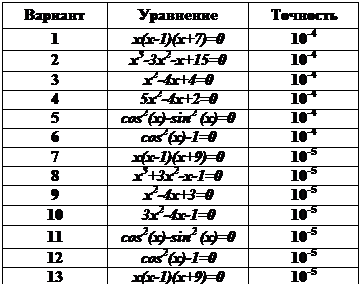
Поиск по сайту: