Тема 2. Введение в теорию измерений

Необходимой составляющей психологического эксперимента (или эмпирического исследования) является измерение, позволяющее перейти от качественного уровня анализа к выявлению количественных соотношений и закономерностей. Иногда в психологии встречаются и сугубо качественные исследования, но они, как правило, имеют место лишь на ранних стадиях изучения проблемы и являются, по сути, предварительным, подготовительным этапом для перехода на более высокий - количественный - уровень.

Кратко рассмотрим некоторые основные понятия, используемые в теории измерений, применяемой в психологии.

Понятия признака и переменной обозначают измеряемые психологические явления и могут рассматриваться как взаимозаменяемые [4. С.11].

С математической точки зрения психологические переменные являются случайными величинами, т.е. такими величинами, про которые заранее неизвестно, какое именно значение они примут в данном конкретном опыте.

Само понятие измерения является глубоко дискуссионным. Широко распространено в психологической литературе определение, принадлежащее С.Стивенсу, в котором под измерением понимается приписывание числовых форм объектам или событиям в соответствии с определенными правилами [10. С.60]. Интерпретируя это определение, О.Ю.Ермолаев отмечает, что измерение – это процедура, с помощью которой измеряемый объект сравнивается с некоторым эталоном и получает численное выражение в определенном масштабе или шкале [3. С.10].

Измерительная шкала задает единицы, эталоны измерения и, в силу этого, является необходимым элементом измерительной процедуры.

Основными типами измерительных шкал, применяемых в психологии, являются следующие:

· номинативная (номинальная, шкала наименований) – шкала, позволяющая классифицировать какие-либо свойства измеряемого объекта, т.е. присвоить им определенные обозначения (числовые, буквенные или иные символьные);

· порядковая (ранговая, ординарная, шкала порядка) – шкала, позволяющая упорядочить получаемое при измерении множество значений признака;

· интервальная (шкала интервалов) – шкала, в которой имеет смысл разность («расстояние») между отдельными измеренными значениями признака;

· отношений (шкала равных отношений) - шкала, в которой имеет смысл отношение измеренных значений признака.

Традиционными трудностями психологических исследований является фактическое отсутствие естественных интервальных шкал и, тем более, шкал отношений для психологических переменных. Для преодоления этих трудностей разработаны специальные математические процедуры, позволяющие построить интервальные шкалы для психологических признаков. Наиболее распространенными примерами таких шкал являются:

· шкала стэнов (sten – сокр. англ. standard ten – стандартная десятка): десятибальная шкала, имеющая по пять делений по обе стороны от среднего значения, равного 5,5, и стандартное отклонение, равное 2 [1. С.80];

· шкала стэнайнов (станайнов) (stenine – сокр. англ. standard nine – стандартная девятка): девятибальная шкала, имеющая среднее значение, включенное в шкалу и равное 5, по четыре деления по обе стороны от среднего и стандартное отклонение, приблизительно равное 2 [1. С.79];

· различные процентильные шкалы [1. С.75-77].

Искусственное происхождение этих шкал «окупается» возможностями по использованию для данных, измеренных в этих шкалах, большого количества глубоко теоретически обоснованных математических методов.

Психолог-экспериментатор обычно имеет дело с выборкой людей, отобранной из значительно большей по численности группы, которая называется генеральной совокупностью. Конечной целью психологического исследования часто является распространение выводов, полученных на выборке, на всю изучаемую генеральную совокупность. В таком распространении знания неоценимую помощь оказывают статистические методы.

Выборки называется независимыми (несвязанными), если процедура проведения эксперимента и полученные результаты измерения некоторого свойства у испытуемых одной выборки не оказывают влияния на особенности протекания этого же эксперимента и результаты измерения этого же свойства у испытуемых другой выборки. Если, напротив, такое влияние имеет место, то выборки называются зависимыми (связанными) [3. C.30-31].

Важнейшим требованием, предъявляемым к выборке, является требование репрезентативности, позволяющее распространить полученные на выборке выводы на всю генеральную совокупность. Репрезентативность выборки означает ее способность «представлять», замещать в процессе познания всю исследуемую генеральную совокупность. Другими словами, репрезентативная выборка представляет собой меньшую по размеру, но достаточно точную модель той генеральной совокупности, которую она должна отражать. На практике добиться репрезентативности выборки часто нелегко, хотя для этого разработан ряд приемов, основными из которых являются следующие:

· Представленность в выборке всех основных признаков генеральной совокупности в той же пропорции и с той же частотой, с которой данный признак встречается в генеральной совокупности. Сложностями такого подхода является частое отсутствие знаний и о том, какие признаки респондентов являются «основными» (существенными для изучаемого явления), и о том, каково распределение этих основных признаков в генеральной совокупности.

· Рандомизация – случайный отбор респондентов из генеральной совокупности. Имеется в виду, что при случайном отборе в выборку попадут респонденты, имеющие всевозможные свойства генеральной совокупности, в том числе – и те, которые существенны для изучаемого психического явления (основные для данного исследования). Однако для этого объем выборки должен быть достаточно большим, причем для точного определения требуемого объема опять же необходимо априорное знание о распределении основных признаков в генеральной совокупности.

Таким образом, ни один из этих способов обеспечения репрезентативности выборки не свободен от недостатков, однако их применение все же целесообразно, так как, без сомнения, повышает достоверность выборочного метода.

Как уже отмечалось, с точки зрения математической теории измеряемые признаки представляются как случайные величины, а для описания таких величин используются законы распределения вероятностей принимаемых данной величиной значений (или коротко – законы распределения).

Наиболее важным законом распределения является нормальный закон (закон Гаусса) в котором плотность распределения вероятностей задается следующим соотношением [5. С.169]:

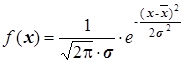, (2-1)

где - функция плотности распределения вероятностей,

- среднеквадратическое отклонение,

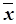- среднее значение признака .

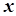Различные полезные для практического применения характеристики нормального распределения приведены, например, в «Словаре-справочнике по психодиагностике» Л.Ф.Бурлачука, С.М.Морозова [2. С.451].

Считается, что нормальное распределение имеет место для явлений, обусловленных большим количеством разнородных и разнонаправленных независимых факторов. Такое объяснение нормального закона имеет под собой глубокие теоретико-математические обоснование (см., напр., [5. С.169-171]), однако среди специалистов до сих пор продолжаются дискуссии о правомерности использования нормального закона в психологии, социологии и других гуманитарных и социально-экономических науках. Тем не менее, на практике значение нормального закона для психолога-экспериментатора состоит в следующем: если полученные данные подчиняются нормальному закону, то для их обработки исследователь может применять множество глубоко обоснованных математических методов (например, параметрические методы проверки гипотез); в противном случае класс допустимых математических методов существенно сужается.

Более подробно методологические и статистические основы теории измерений рассмотрены во многих работах, поэтому предлагаемый список рекомендуемой литературы не претендует на полноту и ориентирован на предоставление читателю возможностей для изучения материала на различных уровнях: элементарное и достаточное для первого знакомства введение можно найти в [1-4]; более строгое изложение имеется, например, в фундаментальном справочнике [5]; отдельные вопросы теории измерений удачно изложены в [6-11].

Вопросы для самопроверки по теме 2

1. Какова роль измерения в психологических исследованиях?

2. Как определяется понятие измерения?

3. Как определяются в теории измерений признак, случайная величина, измерительная шкала?

4. Какие типы измерительных шкал используются в психологических исследованиях?

5. Какие основные процедуры построения интервальных шкал применяются в психологии?

6. Что такое выборка и генеральная совокупность?

7. В чем состоит репрезентативность выборки?

8. Какие способы обеспечения репрезентативности выборки применяются в психологии? В чем их недостатки?

9. Как определяется нормальный закон распределения? Какова его роль в психологических исследованиях?

Рекомендуемая литература по теме 2

Основная

1. Анастази А., Урбина С. Психологическое тестирование. – СПб.: Питер, 2001. – 688 с. – (Серия «Мастера психологии»).

2. Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. – СПб.: Питер, 2000. – 528 с. – (Серия «Мастера психологии»).

3. Ермолаев О.Ю. Математическая статистика для психологов: Учебник. – М.: Московский психолого-социальный институт: Флинта, 2002. – 336 с. – (Библиотека психолога). – Глава 1. Понятие измерения. – С.10-28.; Глава 2. Понятие выборки. – С.29-35; Глава 3. Формы учета результатов наблюдений. – С.36-42.; Глава 4. Числовые характеристики распределений. Нормальное распределение. – С.43-55.

4. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: Речь, 2000. – 350 с. – Глава 1. Основные понятия, используемые в математической обработке психологических данных: 1.1 Признаки и переменные; 1.2. Шкалы измерения; 1.3. Распределение признака. Параметры распределения. – С.11-23.

Дополнительная

5. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание. – М.: Финансы и статистика, 1983. – 471 с.

6. Большой психологический словарь / Сост. и общ. ред. Б.Мещеряков, В.Зинченко. – СПб.: прайм-ЕВРОЗНАК, 2003. – 672 с. - (Проект «Психологическая энциклопедия»).

7. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. – М.: Прогресс, 1976. – 495 с.

8. Мельников В.М., Ямпольский Л.Т. Введение в экспериментальную психологию личности: Учеб. пособие. – М.: Просвещение, 1985. – 319 с.

9. Практикум по общей, экспериментальной и прикладной психологии: Учеб. пособие / В.Д.Балин, В.К.Гайда, В.К.Гербачевский и др. // Под общей ред. А.А.Крылова, С.А.Маничева. Изд-е 2-е, доп. и перераб. – СПб.: Питер, 2000. – 560 с. – («Практикум по психологии»).

10. Стивенс С. Математика, измерение и психофизика // Экспериментальная психология (под ред. С.С.Стивенса) / Пер с англ. под ред. П.К.Анохина, В.А.Артемова. – М.: Иностранная литература, 1960. Т.1. - С.19-92.

11. Суходольский Г.В. Основы математической статистики для психологов. – Л.: Изд-во ЛГУ, 1972. – 429 с.

12. Добавить по алфавиту (скорее всего – в Дополнительную), т.к. хороший матриал!!!!!!!!!!!!!! Боровиков В. STATISTICA: искусство анализа данных на компьютере: Для профессионалов. – СПб.: Питер, 2001. – 656 с. - №6 – Глава 2. Элементарные понятия анализа данных. – С.107-137; - Глава 3. Вероятностные распределения и их свойства. – С.138-176. – Глава 4. Подгонка вероятностных распределений к реальным данным. – С.177-199.

Поиск по сайту: