 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Непараметрические критерии проверки гипотез
| Название | Назначение: оценка достоверности… |
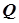 -критерий Розенбаума -критерий Розенбаума
| различий в уровне признака для двух несвязанных выборок |
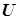 -критерий Манна-Уитни -критерий Манна-Уитни
| |
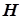 -критерий Крускала- Уоллиса -критерий Крускала- Уоллиса
| различий в уровне признака для трех и более несвязанных выборок |
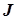 - критерий Джонкира - критерий Джонкира
| тенденции изменения уровня признака для трех и более несвязанных выборок |
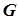 -критерий знаков -критерий знаков
| сдвига значений признака для двух связанных выборок |
 -критерий Вилкоксона -критерий Вилкоксона
| |
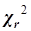 -критерий Фридмана -критерий Фридмана
| сдвига значений признака для трех и более связанных выборок |
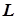 -критерий Пейджа -критерий Пейджа
| тенденции изменения уровня сдвига значений признака для трех и более связанных выборок |
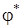 -критерий (угловое преобразование) Фишера -критерий (угловое преобразование) Фишера
| Многофункциональный статистический критерий |
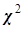 -критерий Пирсона -критерий Пирсона
|
При выводе о статистических гипотезах возможны четыре варианта решения относительно нулевой гипотезы (рис. 3-1):
|
Рис. 3-1. Варианты решения о нулевой
статистической гипотезе
Первый и четвертый варианты решения - правильные, а второй и третий – ошибочные, соответствующие ошибкам первого и второго рода. Ошибку первого рода исследователь совершает, если отклоняет верную нулевую гипотезу 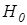 . Ошибка второго рода состоит в принятии ложной нулевой гипотезы
. Ошибка второго рода состоит в принятии ложной нулевой гипотезы 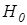 . Соотношения между справедливостью гипотез, принимаемым исследователем решением и этими ошибками показаны в табл. 3-3.
. Соотношения между справедливостью гипотез, принимаемым исследователем решением и этими ошибками показаны в табл. 3-3.
Таблица 3-3
Ошибки первого и второго рода
при статистических выводах
| Решение | Статистические гипотезы | |
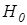 - верна - верна
| 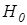 - неверна - неверна
| |
Отклонение 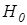 (принятие (принятие  ) )
| Ошибка первого рода | Верное решение |
Принятие 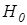 (отклонение (отклонение 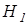 ) )
| Верное решение | Ошибка второго рода |
Обозначим через 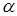 вероятность ошибки первого рода, а через
вероятность ошибки первого рода, а через 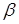 - второго. Необходимо заметить, что в психологической литературе широко применяется следующее фактическое соглашение: под уровнем значимости статистики критерия, равно, как и под уровнем достоверности вывода о справедливости статистических гипотез (будем обозначать их через
- второго. Необходимо заметить, что в психологической литературе широко применяется следующее фактическое соглашение: под уровнем значимости статистики критерия, равно, как и под уровнем достоверности вывода о справедливости статистических гипотез (будем обозначать их через 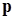 ), часто понимают величину ошибки первого рода
), часто понимают величину ошибки первого рода 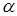 , хотя более корректным является подход, при котором
, хотя более корректным является подход, при котором 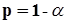 . В результате в разных источниках можно встретить оценки уровня достоверности вывода и 0,95, и 0,05, обозначающие, по сути, одно и то же. Обычно смысл применения понятий «уровень достоверности» и «уровень значимости» ясен из контекста работ. В рамках данного пособия мы будем считать, что:
. В результате в разных источниках можно встретить оценки уровня достоверности вывода и 0,95, и 0,05, обозначающие, по сути, одно и то же. Обычно смысл применения понятий «уровень достоверности» и «уровень значимости» ясен из контекста работ. В рамках данного пособия мы будем считать, что:
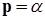 . (3-1)
. (3-1)
В психологических исследованиях обычно в качестве минимально допустимого используют уровень значимости 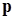 = 0,05.
= 0,05.
Существует несколько способов уменьшения вероятности совершения ошибки первого рода 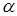 . К ним относятся:
. К ним относятся:
1) увеличение числа наблюдений;
2) увеличение числа серий экспериментов, т.е. повторных измерений, проведенных на одной и той же выборке испытуемых;
3) увеличение уровня значимости, или, другими словами, уровня статистической достоверности вывода.
Рассмотрим влияние увеличения уровня значимости на примере, приведенном в табл. 3-4.
Таблица 3-4
Пример влияния уровня значимости
на результат проверки нулевой гипотезы
Уровень значимости 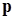
| Результат проверки по 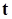 -критерию Стьюдента -критерию Стьюдента
|
| 0,1 | 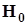 неверна ( неверна (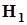 принимается) принимается)
|
| 0,05 | 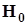 верна ( верна (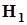 отклоняется) отклоняется)
|
| 0,01 | 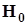 верна ( верна (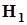 отклоняется) отклоняется)
|
Здесь при 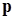 = 0,1 различия между средними, полученные с помощью
= 0,1 различия между средними, полученные с помощью 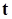 -критерия Стьюдента, являются значимыми, а на самом деле различия - слабые, мы можем ошибочно отвергнуть гипотезу
-критерия Стьюдента, являются значимыми, а на самом деле различия - слабые, мы можем ошибочно отвергнуть гипотезу 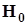 . Увеличивая уровень значимости, мы не получим значимых различий между средними, следовательно, не совершим ошибку первого рода.
. Увеличивая уровень значимости, мы не получим значимых различий между средними, следовательно, не совершим ошибку первого рода.
С понятием ошибки второго рода непосредственно связано понятие мощности критерия проверки гипотез, под которой понимают вероятность не совершить ошибку второго рода, т.е. мощность критерия 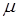 определяется по формуле:
определяется по формуле:
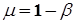 . (3-2)
. (3-2)
Соответственно, чтобы не совершить ошибки второго рода, психолог должен стремиться использовать в исследовании критерий, максимально более мощный для данного класса задач.
Возникает следующий вопрос: какая из этих ошибок, т.е. первого или второго рода, более важна для исследователя, какую из них важнее не допустить? Ответ на этот вопрос неоднозначен и зависит от ряда обстоятельств:
1) от целей, которые преследуются в эксперименте;
2) от предмета изучения и характера исследовательской задачи;
3) от схемы построения исследования.
Например, присяжные, определяя виновность или невиновность подсудимого, должны решить, что более значимо: признать невиновного виновным или наоборот. Установка на гуманность диктует правило: пусть будут оправданы десять преступников, чем пострадает один невиновный. Репрессивная же установка предполагает другое правило: пусть пострадают десять невиновных, лишь бы один виновный не ушел от наказания.
Ошибка первого рода существенна в конфирматорном (уточняющем) эксперименте, а также тогда, когда непринятие верной гипотезы об отсутствии различий имеет практическую значимость: так, принятие ложной гипотезы об интеллектуальных различиях представителей разных социальных страт или этнических групп может иметь серьезные социально-политические последствия.
Ошибка второго рода существенна в эксплораторном (разведочном) эксперименте. Отклонение гипотезы о различиях на начальной стадии может надолго дезориентировать исследователя в отношении изучаемых закономерностей. Поэтому уровень статистической достоверности при проведении эксплораторного эксперимента стремятся понизить, применяя два способа:
1) проведение эксплораторного эксперимента на малых выборках, т.е. уменьшение количества наблюдений;
2) задание невысокого уровня значимости (обычно 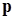 =0,1 или 0,05).
=0,1 или 0,05).
Субъективно исследователю, очевидно, приятнее получить подтверждение своих гипотез, чем их опровержение, поэтому у начинающих психологов вероятность ошибок первого рода значительно выше, чем ошибок второго рода. Следовательно, важно стремиться обезопасить себя, в первую очередь, от ошибок первого рода.
Стратегия экспериментального исследования в любой области психологической науки может быть представлена следующей схемой:
1) переход от эксплораторного эксперимента к конфирматорному;
2) переход от низких уровней достоверности к высоким;
3) переход к исследованиям на больших выборках вместо малых.
Более подробно анализ статистических гипотез рассмотрен в источниках [1-13], которые мы отобрали из огромного количества работ по данной тематике:
· необходимый для психолога минимум знаний изложен в учебных пособиях Е.В.Сидоренко [3] и О.Ю.Ермолаева [2], а также в пользующейся заслуженной популярностью на протяжении многих лет работе [1] Дж.Гласса (Gene V. Glass), Дж.Стэнли (Julian C. Stanley), в которой помимо систематического изложения основ проверки гипотез (глава 13, с.246-264) имеется множество содержательных примеров прикладного применения теории проверки статистических гипотез в психологических и педагогических исследованиях;
· ориентированное на задачи психологического исследования рассмотрение анализа статистических гипотез содержится в книгах Е.Ю.Артемьевой, Е.М.Мартынова [5], В.Н.Дружинина [6], Т.В.Корниловой [8; 9], Г.В.Суходольского [11];
· в качестве справочного руководства весьма полезна фундаментальная работа [4];
· элементарное введение в статистические основания проверки гипотез имеется в работе [7] Грегори Кимбла (Gregory A. Kimble);
· популярное и, в то же время, весьма содержательное рассмотрение как основ, так и конкретных критериев проверки гипотез имеется в работах [12-13] Ю.Н.Тюрина, А.А.Макарова;
· строгий математический аппарат теории проверки гипотез представлен в работе [10] Э.Лемана (E.L.Lehmann), имеющей обширную дополнительную библиографию.
Вопросы для самопроверки по теме 3
1. Какая гипотеза называется статистической?
2. Как классифицируются статистические гипотезы?
3. Какие основные группы методов применяются для проверки статистических гипотез? Как они определяются?
4. Какие условия необходимы для применимости параметрических методов проверки гипотез?
5. Приведите примеры параметрических методов проверки статистических гипотез.
6. Приведите примеры непараметрических методов проверки статистических гипотез.
7. Какие варианты решений относительно нулевой гипотезы возможны при выводе о статистических гипотезах?
8. Как определяются ошибки первого и второго рода при выводе о статистических гипотезах?
9. Приведите примеры способов уменьшения вероятности совершения ошибки первого рода.
10. Как определяется мощность статистического критерия? Как соотносятся между собой по мощности параметрические и непараметрические критерии?
11. Однозначен ли приоритет отслеживания ошибок первого или второго рода? От чего он зависит?
12. В чем состоит общая стратегия проведения эксперимента?
Рекомендуемая литература по теме 3
Основная
1. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. – М.: Прогресс, 1976. – 495 с.
2. Ермолаев О.Ю. Математическая статистика для психологов: Учебник. – М.: Московский психолого-социальный институт: Флинта, 2002. – 336 с. – (Библиотека психолога). – Глава 5. Общие принципы проверки статистических гипотез. – С.56-65.
3. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: Речь, 2000. – 350 с. – Глава 1. Основные понятия, используемые в математической обработке психологических данных: 1.4. Статистические гипотезы; 1.5. Статистические критерии; 1.6. Уровни статистической достоверности; 1.7. Мощность критериев; 1.8. Классификация задач и методов их решения; 1.9. Принятие решения о выборе метода математической обработки. – С.24-36.
Дополнительная
4. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание. – М.: Финансы и статистика, 1983. – 471 с.
5. Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. – М.: Изд-во МГУ, 1975. – 207 с.
6. Дружинин В.Н. Экспериментальная психология. – СПб: Питер, 2000. – 320 с.
7. Кимбл Г. Как правильно пользоваться статистикой / Пер. с англ. Б.И.Клименко. – М.: Финансы и статистика, 1982. – 294 с.
8. Корнилова Т.В. Экспериментальная психология: Теория и методы: Учебник для вузов. - М.: Аспект Пресс, 2002. – 381 с.
9. Корнилова Т.В. Введение в психологический эксперимент. – М.: Изд-во МГУ, 1997. – 256 с.
10. Леман Э. Проверка статистических гипотез / Пер. с англ. Ю.В.Прохорова. – М.: Наука, 1979. – 408 с.
11. Суходольский Г.В. Основы математической статистики для психологов. – Л.: Изд-во ЛГУ, 1972. – 429 с.
12. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. – М.: ИНФРА-М; Финансы и статистика, 1995. – 384 с.
13. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. – М.: ИНФРА-М, 1999. – 528 с.
Поиск по сайту: