Сплайн интерполяция

При большом количестве узлов интерполяции полином имеет высокую степень, что неудобно при вычислениях. Тогда отрезок интерполяции разбивают на части, и на каждой строят интерполяционный многочлен, т. е. выполнят кусочно-линейную интерполяцию. Однако в точках «сшивки» частей первая производная будет иметь разрыв. По этому используют особый вид кусочно-линейной интерполяции – сплайн-интерполяция.

Сплайн – функция, которая на каждом частичном отрезке является алгебраическим многочленом, а на всем отрезке непрерывна в мест с несколькими своими производными. Термин spline – линейка, возник из механической интерпретации: чертежники издавна пользовались упругими, гибкими линейками для проведения гладких кривых через множество заданных точек.

Наибольшее распространение получила кубическая сплайн интерполяция, т. к. кубическая сплайн функция является самой гладкой из функций интерпретирующей заданные точки.

При построении функции на всем интервале интерполяции необходимо определить общее число параметров подлежащих определению, а значит нужно иметь столько же уравнений.

На под интервале между узлами надо построить фрагмент кубических кривых, каждая с 4 параметрами ().

Условие непрерывности S, S`, S`` во всех внутренних узлах дает уравнений.

Далее требуемое совпадение функции во всех 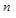узлах дает еще 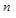уравнений.

а надо => нужны еще 2 условия.

Обычно эти дополнительные условия касаются требований к сплайн функции на концах или вблизи концов сплайна. S`(), S`()

Введем обозначения на интервале .

;

;

.

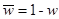Тогда сплайн на этом под интервале представляется формулой

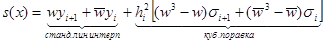
Особенности:

1. и неизвестные константы.

2. Поправочный член в [] равен нулю на концах под интервала.

Тогда ;

Продифференцируем S(x) трижды как сложную функцию.

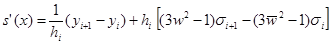
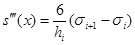
Из приведенных соотношений видно, что S``(x) – линейная функция интерполирующая значения и , значит . Это соотношение проясняет суть соотношения но не определяет его величину, при этом надо помнить, что 3 производная S```(x) – константа на каждом под интервале, а следовательно порядка на интервале равна 0. Вычислим S`(x) на концах под интервала, причем определим односторонние производные на границе.

Для обеспечения непрерывности на всех внутренних узлах, налагается условие s`()=S'_{+}(x_i), i=2,(n-1)

Эта система n-2 линейных уравнений относительно неизвестных коэффициентов , нужны еще 2 условия для однозначность определения интерполяционного сплайна.

Поиск по сайту: