АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Погрешность интерполяции

Читайте также:
  1. А. Средняя квадратическая погрешность функции измеренных величин.
  2. Метод (способ) интерполяции
  3. Относительная погрешность суммы
  4. Погрешность измерений равна половине цены деления шкалы измерительного прибора.
  5. Погрешность измерения
  6. Погрешность по углу
  7. Полная погрешность.
  8. Понятие об интерполяции и экстраполяции уровней динамического ряда
  9. Прогнозирование элементов рынка методом интерполяции динамических рядов
  10. Суммарная погрешность, её состав. Диапазон измерения
  11. Суммарная систематическая погрешность

 

Погрешность вызванную заменой искомой функции 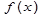интерполяционным многочленами можно записать так.

 

;

 

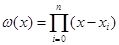
В узлах интерполяции погрешность равна 0. Введем вспомогательную функцию.

 

 

В этой вспомогательной функции 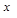играет роль параметра и может принимать любые значения.

 

При

 

Допустим, что 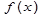и имеют непрерывные производные. Известно, что между двумя 0 гладкой функции лежит 0 ее производной. Применяя последовательно это правило получим, что между крайними из 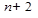нулей функции лежит 0 ее производной.

 

 

Вычислим производную вспомогательной функции

 

.

 

Пусть точка 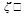лежит между указанными нулями и в этой точке производная = 0.

 

 

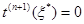
Отсюда

 

 

Заменим погрешность максимально возможной

 

 

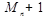– максимум модуля производной.

 

 

Этот максимум берется из наименьшим и наибольшим из

 

Эта оценка погрешности априорная (можно вычислить до выполнения расчетов), а оценка по первому отброшенному члену называется апостериорная (получена в результате расчета). Расчеты показывают, что эти погрешности близки.

 

Приведем формулы для апостериорной оценки погрешности в таблицах с постоянным шагом для первой и второй формул Ньютона.

 

 

для второй формулы Ньютона

 

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)