Сингулярное распределение

Опр.: Распред. с.в. x назыв. сингулярным, если F_x(x) непрерывна, F’_x(x)=0 п.в. на m

(например: лестница Кантора)

Теорема Лебега: Если F(x) удовлетворяет F1-F3, то F(x)≡pF_d(x)+q F_a(x)+r F_s(x), где p+q+r=1; p,q,r≥0,

F_d– ф-ия распределения дискретного типа

F_a– ф-ия распределения абсолютно-непрерывного типа

F_s – ф-ия распределения сингулярного типа

55.Центральная предельная теорема.

1. ЦПТ для одинаково распределенных с.в.

Рассмотрим последовательность независимых и одинаково распределенных с.в. ξ₁, ξ_2,…, ξ_n,…

Обозначим мат. ожидание Eξ_k=a, Dξ_k=σ², через S_n= -частичную сумму.

Согласно ЗБЧ: 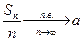. Если в этом соотношении знаменатель заменить на , то при больших значениях n распределение с.в. всегда будет иметь одно и то же нормальное распределение.

Обозначим через F_n(x) – ф. р. с. в. имеет среднее значение 0, а дисперсию -1 "n.

ЦПТ: При n®¥ ф.р. , ( – функция распределения стандартного нормального закона)

Док-во: Не ограничевая общности, можно считать, что мат.ожидание а= 0. Если это не так, то всегда можно перейти от с.в. ξ_i к с.в. ξ_i- a. Поэтому будем рассматривать с.в. .

Воспользуемся теоремой непрерывности для х. ф. и докажем, что с.в. .

Из свойств х. ф. Þ что

.

ЦПТ (для разнораспределенных с.в.): Если , а , то при выполнении условия Линдеберга сумма сходится при n®¥ к стандартному нормальному распределению или что тоже сходится к нормальному распределению.

53.Аксиомы теории вероятностей. Примеры моделей, реализующих систему аксиом.

Опр1: Вероятностным пространством называют тройку <Ω, A,P>, где Ω – произвольное множество, A – алгебра подмножеств, P – нормированная мера на A.

Аксиомы алгебры:

А1: Если АÎ 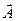, то и Î A, =W\ A

А2: Если A, BÎ A, то AÈBÎ A и AÇBÎ A

Алгебра А называется s-алгеброй, если аксиома А2 выполняется и для счетного числа подмножеств.

Если на Ω введена s-алгебра А, то на этом пространстве определен план событий, замкнутый относительно ÇÈ`.

Аксиомы вероятности:

Р1: "AÎ A P(A)≥0

Р2: P(Ω)=1

Р3: A₁,A₂,…,A_n ÎA (счетная посл-ть)ÞP = 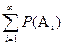– свойство счетной аддитивности.

Вероятностное пространство является мат. Моделью любого случайного эксперимента. Ω будет пониматься как множество, состоящее из возможных исходов случайного эксперимента; отдельные исходы будем обозначать wÎW.

Если рассмотреть эксперимент с подбрасыванием игральной кости, то Ω={1,…,6}.

Если Ω – счетное множество, то вероятностное пространство называется дискретным.

Каждое множество AÎ A будем называть случайным событием.

Если wÎА будем говорить, что событие А произошло.

1. Если А и В – два случайных события, то АÇВ называет произведением событий и обозначают АВ. Оно наступит когда наступит каждое из событий: wÎАÇВ Û wÎА и wÎВ.

2. АÈВ называют суммой событий; оно научит тогда, когда наступит хотя бы одно из них: wÎАÈВÛwÎА или wÎВ.

3. – событие, противоположное к событию А (когда не наступит А).

4. А\В – разность событий А и В: wÎА\В Û wÎА и wÏВ.

5. Æ – невозможное событие, Ω – достоверное событие.

Опр: Событие А₁, А₂,… образуют полную группу событий, если А_iÇ А_j=Æ, i¹j и .

Опр: Если АÇ А=Æ, то называются несовместными.

Поиск по сайту: