Свойства вероятностей

1. P(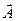)=1-P(A)

2. P(Æ)=0

3. AÌBÞP(A)£P(B)

4. P(AÈB)=P(A)+P(B)-P(AÇB)

P(AÈBÈC)=P(A)+P(B)+P(C)-P(AÇB)-P(BÇC)-P(AÇC)+P(AÇBÇC)

5. Свойство непрерывности вероятностей:

Если A_nÉA_n+1É… – убывающая последовательность событий и 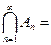Æ, то .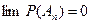

5’. A_nÉA_n+1É…, 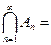A, то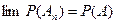

5’’ A_nÌA_n+1Ì…, 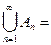A, то .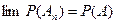

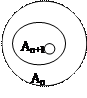Док-во5: A_n=(A_n\A_n+1)È(A_n+1\A_n+2)È…

A_n+1=(A_n+1\A_n+2)È…

54. Распределение случайной величины. Основные типы распределений.

Опр1: Борелевской -алгеброй на прямой называют наименьшую -алгебру, содержащая все интервалы числовой прямой. Алгебру обозначим через B, элементы будем называть борелевскими множествами BÎ B.

Примеры:

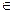1) Одноточечное мн-во {a} является борел., т.к. его можно представить в виде {a}= ,{a} B

2) 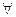открытое мн-во G на прямой

3) 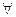замкнутое мн-во F 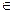B, т.к. F=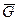

Пусть дано <W,A,P>-вероятностное пространство.

Опр2:. Случайной величиной называется измеримое отображение пространства исходов в числовую прямую, x: W®R. Для любого борелевского множества B 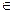B на числовой прямой множество исходов {w: x(w) 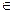B}Î A.

Вопрос: Зачем нужна измеримость? Если с.в. x измерима в указанном смысле, то это означает, что можно всегда найти вероятность того, что с.в. x попадет в произвольное борелевское множество В P({w: x(w) 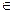Bx})=P(x 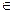B).

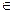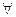Опр3: Распределением с.в. x называют физическую функцию определенную на всех борелевских множествах числовой прямой равенством: P_x(B)=P(x B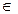) B B.

Легко проверить, что распределение с.в. является вероятностной мерой на борелевской -алгебре, а тройка <R, B, P_x> является вероятностным пространством.

Рассмотрим множество B_x=(-¥,x), xÎR. Вычислим P(B_x)=P(xÎ(-¥,x))=P(x<x)

Опр4: Функцией распределения сл.в. x называют функцию F(x), определенную на всей числовой прямой, F_x(x)=P(x<x), т.е. F_x(x)=P((- ,x))

Функция распределения однозначно определяет распределение с.в. x.

Св-ва ф-ии распред.:

F1) Ф. распр.- неубывающая ф-ия

F2) Ф распр. непр слева, т.е. для любой последовательности {x_n} $x₀: F_x(x_n)®F_x(x₀)

F3) F_x (+ ) =1; F_x (- ) =0.

Эти три св-ва однозначно определяют ф-ию распределения и назыв. характеристическими св-ми ф. распр.

4) P(a≤x<b)=F_x(b)-F_x(a)

P(a≤x£b)=F_x(b+0)-F_x(a)

P(a<x<b)=F_x(b)-F_x(a+0)

P(a<x£b)=F_x(b+0)-F_x(a+0)

5) 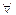x 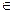R P(x=x)=F_x(x+0)-F_x(x). Вероятность принять значение х равна величине скачка функции распределения в т. х. Поэтому, если в т х ф.р. непрерывна, то это значение х принимается с вероятностью 0.

Основные типы распределений:

Опр.: Борелевское мн-во S на числ. прямой назыв. носителем с.в. x, если P_x(S)=1.(на этом мн-ве сосредоточена вся един. масса распределения). При этом под носителем будем понимать самое маленькое мн-во удовл. этому св-ву.

Опр.: Распределение с.в. x называется дискретным, если носитель этого распределения не более чем счетное множество на числовой прямой, а саму с.в. x называют дискретной

S={x₁,x₂,…,x_n}, x 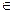S, P(x=x_k)=P_k, SP_k=1

Соотв. этому распред. с.в. назыв. дискретной.

Поиск по сайту: