 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Применение законов сохранения энергии. Условия механического равновесия
Согласно первому закону механики тело находится в состоянии покоя, если на него не действуют силы или их равнодействующая равна нулю.
Сила 
, действующая на тело, связана с изменением потенциальной энергии 
.
Для одномерного случая
.
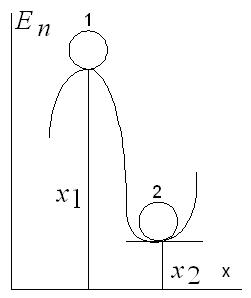
Рис. 2.6. Устойчивое (1) и неустойчивое (2) равновесия
Если в состоянии равновесия сила равна нулю, то 
, т. е. в точке равновесия потенциальная энергия либо максимальна либо минимальна х2 (рис. 2.6).
В положении 1 на тело, выведенное из положения равновесия, будет действовать сила, уводящая тело от положения равновесия.
В положении 2 сила будет возвращать тело в положение равновесия.
В первом случае положение неустойчивое
; 
.
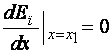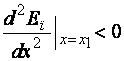Во втором случае равновесие устойчивое
; 
.
Г р аницы движения. Из закона сохранения механической энергии следует, что потенциальная энергия Еп не может быть больше полной энергии W, так как кинетическая энергия всегда положительна
; 
.
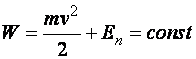Поэтому тело, имеющее определённое значение полной энергии, может находиться только в тех точках поля, где его потенциальная энергия меньше (или равна) полной.
Пример. Пусть потенциальная энергия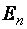 
зависит от координаты 
по закону квадратичной параболы 
.
Максимальное значение потенциальной энергии не может быть больше 
:
,
т. е. тело не может выйти за интервал, ограниченный значениями 
и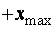 
. Потенциальная кривая, отражающая зависимость 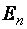от , напоминает «яму», отсюда термин «потенциальная яма».
Рис. 2.7. Потенциальная яма
Рис. 2.8. Потенциальный барьер
Можно легко представить себе вполне реальное движение, при котором потенциальная кривая имеет вид, изображенный на рис. 2.7 (максимальное значение 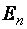равно N) Возьмем желоб такой формы, как потенциальная кривая, и пусть по нему катится шарик. Потенциальная энергия шарика 
. Перемещаясь по желобу, шарик будет иметь потенциальную энергию, соответствующую высоте данной точки желоба. Если нет потерь энергии, шарик будет перемещаться с левой ветви на правую и наоборот, поднимаясь каждый раз на одну и ту же начальную высоту. Проекция на ось будет совершать колебательное движение.
Если взять более сложный вид потенциальной кривой (рис. 2.8), то и здесь можно найти области, недоступные для движения: 0 – 
, 
– 
. При заданном уровне полной энергии W тело, находящееся в пределах от до , не может выйти из этой потенциальной ямы. Для того чтобы попасть в зону > , необходимо преодолеть барьер высотой 
. Для этого полная энергия должна быть больше .
12 вопрос
2.1. Определение момента инерции
Момент инерции J (кгм2) – параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: 
.
Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры[1].
Моменты инерции однородных тел простых форм приведены в табл. 2.1.
Таблица 2.1
Поиск по сайту: