Моменты инерции некоторых однородных тел

Диск или цилиндр вращающийся вокруг центральной оси
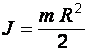
Момент инерции стержня при вращении относительно оси, проходящей через его конец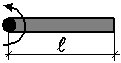
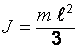
Момент инерции стержня при вращении относительно оси, проходящей через его центр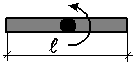
Момент инерции шара при вращении относительно оси, проходящей через его центр

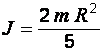
Момент инерции тела, если известно распределение массы тела относительно оси вращения m_i (R), может быть определён как

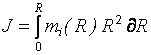. (2.11)

Детали электропривода, например ротор электрической машины, представляют собой конструкции, состоящие из деталей сложных форм и изготовленные из материалов различной плотности. Следовательно, расчёт момента инерции связан со значительными трудностями.

В случаях, когда расчёт момента инерции не возможен либо затруднён, используют следующие методы экспериментального определения момента инерции.

Метод свободного выбега (самоторможения) ^[2]. Сущность этого метода состоит в следующем. Исследуемый агрегат, включающий в себя электродвигатель и механически соединённые с ним элементы, разгоняется до некоторой установившейся частоты вращения в режиме х.х. . После этого электродвигатель отключают от сети и наступает процесс самопроизвольного торможения, т.е. торможения исключительно за счёт внутренних сил трения в подшипниках электродвигателя и сочленённых с ним вращающих частей о воздух. На преодоление этих сил трения затрачивается кинетическая энергия (Дж), запасенная во вращающихся частях агрегата:

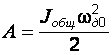. (2.12)

С другой стороны, эта энергия может быть определена как произведение мощности, затраченной на приведение во вращение агрегата в режиме х.х. 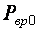на время :

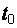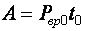. (2.13)

Приравняв (9.1) к (9.2), получим выражение общего момента инерции, кг·м²:

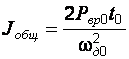. (2.14)

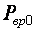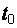Значения и определяют экспериментально, выполнив опыт х.х. и опыт свободного выбега, по кривой выбега: .

Метод вспомогательного маятника. Этот метод применяют в тех случаях, когда метод свободного выбега не может быть использован, в частности для электрических машин большой мощности – до 1000 кВт.

Для реализации этого метода вращающуюся часть машины устанавливают на подшипниках балансировочного станка. Если вращающаяся часть машины имеет собственные подшипники, то могут быть использованы и они. Испытания проводят на собственной машине. У коллекторных машин или асинхронных двигателей с фазным ротором при определении момента инерции следует поднять щётки.

При использовании метода вспомогательного маятника к валу исследуемой вращающейся части прикрепляют дополнительную массу m_доп центр тяжести которой находится на расстоянии а от центра вала.

Вращающуюся часть вместе со вспомогательным маятником следует привести в колебательное движение. При этом одностороннее угловое отклонение не должно превышать 15^о. Период колебаний принимают как средний из нескольких колебаний. Для точности рекомендуется производить измерения периода колебаний в момент нахождения маятника через положение статического равновесия.

Момент инерции испытуемой вращающейся части определяется по формуле

. (2.15)

Для повышения точности измерения момента инерции рекомендуется проводить измерения несколько раз с разными значениями дополнительной массы вспомогательного маятника m_доп или расстояния

Динамика вращательного движения твердого тела. Момент силы. Момент инерции. Теорема Штейнера. Момент импульса. Основной закон вращательного движения.
Динамика вращательного движения твердого тела.
Вращательное действие силы характеризуется моментом силы относительно точки (рис. 5а) и относительно оси (рис. 5б). Для того чтобы определить момент силы 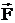относительно точки О, проведем из точки О радиус-вектор 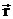в точку приложения силы (рис. 5а). Моментом силы 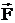относительно точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора 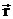на силу :

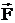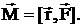
Модуль момента силы M=r×F×sina=F×d, гдеd=r×sina – плечо силы.
Для того чтобы определить момент силы 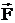относительно оси Z, выберем на оси Z произвольную точку, найдем момент силы относительно этой точки, а затем спроецируем на ось Z момент силы относительно точки. Таким образом, момент силы относительно оси – величина скалярная.
Разложим силу на три составляющие (рис. 5б):
– осевая, параллельная оси вращения,
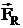– радиальная, перпендикулярная оси вращения,
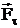– касательная, перпендикулярная 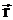и оси вращения.
Составляющую 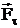можно определить как проекцию силы 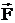на направление вектора 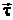, направленного по касательной к окружности радиусом R, проведенной через точку приложения силы перпендикулярно оси вращения. Направление вектора 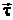образует с осью Z правовинтовую систему.
Составляющие 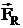и вращения тела относительно оси Z не вызывают. Вращающее действие силы 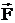обусловлено составляющей 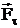. Можно показать, что момент силы 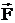относительно оси Z

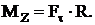
Инертные свойства тела при вращательном движении характеризует м омент инерции. Он зависит от распределения массы тела относительно оси вращения. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси: .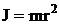

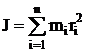– момент инерции системы материальных точек;

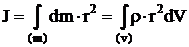– момент инерции тела, где 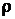– плотность тела.

ТЕОРЕМА ШТЕЙНЕРА
рис 6.
Момент инерции тела относительно произвольной оси может быть рассчитан по теореме Штейнера: момен тинерции тела относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр инерции и параллельной O'O, и произведения массы тела на квадрат расстояния между осями (рис. 6):

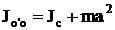
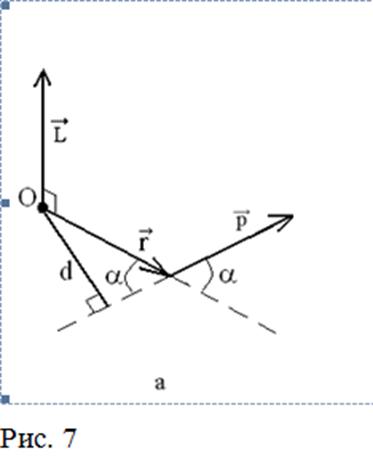
Моментом импульса материальной точки относительно некоторой точки называется векторная величина, равная векторному произведению радиуса-вектора 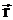на импульс материальной точки (рис. 7а):


.

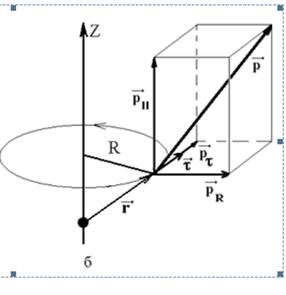
Моментом импульса системы материальных точек называется геометрическая сумма моментов импульсов точек, составляющих систему:

.

Моментом импульса материальной точки относительно осиZназывается скалярная величина, равная проекции момента импульса относительно произвольной точки, лежащей на осиZ, на эту ось. Аналогично моменту силы относительно оси, момент импульса относительно осиZ

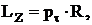
где pt – проекция импульса на направление вектора 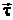, направленного по касательной к окружности радиусом, проведенной через материальную точку перпендикулярно оси вращения (рис. 7б). Направление вектора 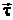образует с осью Z правовинтовую систему.
Момент импульса тела относительно оси вращения

LZ=IZ×wZ,

где IZ – момент инерции тела относительно оси Z, wZ – проекция угловой скорости тела на ось Z. Для однородного тела, вращающегося относительно оси симметрии:

.
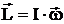Основной закон динамики вращательного движения:
Скорость изменения момента импульса тела относительно оси равна результирующему моменту внешних сил относительно этой же оси (проекция углового ускорения на ось пропорциональна результирующему моменту внешних сил относительно оси и обратно пропорциональна моменту инерции тела относительно этой же оси):

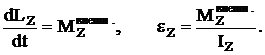
Из законов динамики поступательного и вращательного движений следует условие равновесия тел:

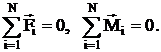
Поиск по сайту: