 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Классификация термодинамических процессов
| Процесс | Условия |
| Изотермический | Постоянная температура – T = const |
| Изобарный | Постоянное давление – p = const |
| Изохорный | Постоянный объем – V = const |
| Адиабатический | Отсутствие теплообмена между системой и внешней средой – d Q =0 |
Первое начало термодинамики, или закон сохранения энергии, гласит, что энергия не может возникать из ничего и исчезать, а только переходит из одной формы в другую. Например, внутренняя энергия, содержащаяся в веществе, может превращаться в тепловую, световую (пламя), электрическую (химический аккумулятор) и т.д.
Например, сообщим системе некоторое количество тепловой энергии Q, котораярасходуется на совершение работы A и на изменение состояния внутренней энергии системы D U:
Q = A + D U (7.1),
где D U – изменение величины, которую называют внутренней энергией системы. Если система совершает работу за счет внутренней энергии без поступления теплоты, то A = –D U (адиабатический процесс).
Таким образом, увеличению внутренней энергии системы соответствуют положительные значения D U, уменьшению – отрицательные значения. Теплота, сообщаемая системе, и работа, совершаемая системой, также считаются
положительными, и наоборот, теплота, отдаваемая системой, и работа, совершаемая над системой, считаются отрицательными.
Внутренняя энергия относится к функциям состояния, т.е. величинам, которые зависят только от состояния системы и не зависят от ее предыстории. Следовательно, изменение внутренней энергии в ходе процесса зависит только от начального и конечного состояния и не зависит от пути протекания процесса. Напротив, работа зависит от пути протекания процесса, и поэтому не обладает свойствами функции состояния, как «запас работы», которую может совершить система.
Единицей измерения работы, теплоты и внутренней энергии в системе СИ служит джоуль (Дж). 1 джоуль – это работа силы в 1 ньютон на расстоянии 1 м (1 Дж = 1 Н×м = 1 кг×м2/с2). В старой химической литературе широко использовалась единица количества теплоты и энергии калория (кал). 1 Калория – это такое количество теплоты, которое необходимо для нагревания 1 г воды на 1°C. 1 Кал = 4,184 Дж» 4,2 Дж. Теплоты химических реакций удобнее выражать в кило-джоулях или килокалориях: 1 кДж = 1000 Дж, 1 ккал = 1000 кал.
§ 3. Закон Гесса. В химической термодинамике первый закон трансформируется в закон Гесса,характеризующий тепловые эффекты химических реакций.Теплота, как и работа, не является функцией состояния. Поэтому для придания тепловому эффекту свойства функции состояния введена энтальпия (D H), направленное изменение которой составляет D H = D U + P D V при постоянном давлении. Отметим при этом, что P D V = A – работе расширения, а D H = –Q (с обратным знаком). Энтальпию характеризуют теплосодержанием системы так, что экзотермическая реакция понижает D H. Обратите внимание, что выделению теплоты в химической реакции (экзотермической) соответствует D H < 0, а поглощению (эндотермической) D H > 0. В старой химической литературе была принята противоположная система знаков (!) (Q > 0 для экзотермических реакций и Q < 0 для эндотермических).
Изменение энтальпии (тепловой эффект) не зависит от пути реакции, а определяется только свойствами реагентов и продуктов (закон Гесса, 1836)
Покажем это на следующем примере:
C(графит) + O2(г.) = CO2(г.) D H 1 = –393,5 кДж
С(графит) + 1/2 O2(г.) = CO(г.) D H 2 = –110,5 кДж
СО(г.) + 1/2 O2(г.) = СО2(г.) D H 3 = –283,0 кДж
Здесь энтальпия образования CO2 не зависит от того, протекает ли реакция в одну стадию или в две, с промежуточным образованием CO (D H 1 = D H 2 + D H 3). Или иными словами сумма энтальпий химических реакций в цикле равна нулю:
rot  (7.2),
(7.2),
где i – число реакций в замкнутом цикле.
В любом процессе, когда конечное и начальное состояния веществ одинаковы, сумма всех теплот реакции равна нулю.
Например, мы имеем последовательность из нескольких химических процессов, приводящих в конце к исходному веществу и характеризующихся каждый своей энтальпией, т.е.
 (7.3)
(7.3)
то, согласно закону Гесса,
D H 1 + D H 2 + D H 3 + D H 4 = 0 (7.4)
Результирующий тепловой эффект равен нулю потому, что на одних стадиях тепло выделяется, на других – поглощается, что приводит к взаимной компенсации.
Закон Гесса позволяет вычислить тепловые эффекты тех реакций, для которых прямое измерение невозможно. Например, рассмотрим реакцию:
H2(г.) + O2(г.) = H2O2(ж.) D H 1 =?
Экспериментально легко измерить следующие тепловые эффекты:
H2(г.) + 1/2O2(г.) = H2O(ж.) D H 2 = –285,8 кДж
H2O2(ж.) = H2O(ж.) + 1/2O2(г.) D H 3 = –98,2 кДж
Пользуясь этими значениями, можно получить:
D H 1 = D H 2 – D H 3 = –285,8 + 98,2 = –187,6 (кДж/моль).
Таким образом, достаточно измерить тепловые эффекты ограниченного числа реакций, чтобы затем теоретически вычислить тепловой эффект любой реакции. На практике табулированы стандартные энтальпии образования D Hf °298, измеренные при Т =298,15 К (25°C) и давлении p = 101,325 кПа (1 атм), т.е. при стандартных условиях. (Не путать стандартные условия с нормальными!)
Стандартная энтальпия образования D Hf ° – это изменение энтальпии в ходе реакции образования 1 моля вещества из простых веществ:
Ca (тв.) + C (графит) + 3/2O2 (г.) = CaCO3 (тв.) D H °298=–1207 кДж/моль.
Обратите внимание, что в термохимическом уравнении указываются агрегатные состояния веществ. Это очень важно, т.к. переходы между агрегатными состояниями (фазовые переходы) сопровождаются выделением или поглощением тепла:
H2 (г.) + 1/2O2 (г.) = H2O (ж.) D H °298 = –285,8 кДж/моль,
H2 (г.) + 1/2O2 (г.) = H2O (г.) D H °298 = –241,8 кДж/моль.
H2O (г.) = H2O (ж.) D H °298 = –44,0 кДж/моль.
Стандартные энтальпии образования простых веществ приняты равными нулю. Если простое вещество может существовать в виде нескольких аллотропных модификаций, то D H ° = 0 приписывается самой устойчивой при стандартных условиях форме, например, кислороду, а не озону, графиту, а не алмазу:
3/2O2 (г.) = O3 (г.) D H °298 = 142 кДж/моль,
C (графит) = C (алмаз) D H °298 = 1,90 кДж/моль.
Следствием закона Гесса с учетом изложенного тогда изменение энтальпии в ходе реакции, будет равно сумме энтальпий образования продуктов за вычетом суммы энтальпий образования реагентов с учетом стехиометрических коэффициентов реакции:
D H (реакции) = SD Hf (продуктов) – SD Hf (реагентов) (7.5)
Вычислим стандартную энтальпию реакции:
4Al (тв.) + 3PbO2 (тв.) = 2Al2O3 (тв.) + 3Pb (тв.) (a)
Стандартные энтальпии образования найдем по справочным данным:
2Al (тв.) + 3/2O2 (г.) = Al2O3(тв.) D H °298 = –1669,8 кДж/моль, (b)
Pb (тв.) + O2 (г.) = PbO2 (тв.) D H °298 = –276,6 кДж/моль. (c)
С термохимическими уравнениями можно обращаться так же, как и с алгебраическими: умножать на число, складывать, вычитать, переносить слагаемые из одной части в другую.
4Al (тв.) + 3O2 (г.) + 3Pb (тв.) + 3O2 (г.) = 2Al2O3 (тв.) + 3PbO2 (тв.)
D H °298(a) = 2×D H °298(b) – 3×D H °298(c)
4Al (тв.) + 3PbO2 (тв.) = 2Al2O3 (тв.) + 3Pb (тв.)
D H °298(a) = 2×(–1669,8)–3×(–276,6) = –2509,8 кДж.
Обратите внимание, что свободный кислород, не участвующий в реакции, сократился при преобразованиях. На самом деле нет необходимости записывать расчеты так подробно. Если стехиометрические коэффициенты подобраны правильно, то баланс по всем веществам обязательно сойдется. Более кратко расчет D H реакции записывают так:
4Al(тв.) + 3PbO2(тв.) = 2Al2O3(тв.) + 3Pb(тв.)
Δ Hf °298 0 3×(–276,6) 2×(–1669,8) 0
D H °298 = 2×(–1669,8)–3×(–276,6) = –2509,8 кДж.
Цикл Борна – Габера. Важным развитием и следствием закона Гесса является установление взаимосвязи между термодинамическими параметрами реакции, химических соединений и энергетическими параметрами атома, молекулы (потенциал ионизации, энергия сродства к электрону, энергия хим. связи, кристаллической решетки и др.). Так, в «Практикуме по общей химии» и в других учебниках дан пример взаимосвязи потенциала ионизации атома натрия (I Na), энергий диссоциации молекулы хлора (D Hдисс), сублимации (атомизации) натрия (D H ат), сродства к электрону (E Cl), кристаллической решетки хлорида натрия (U) и собственно энтальпии образования хлорида натрия (D H обр). Так что можно
записать
D H обр = D H ат + I Na +  D Hдисс + E Cl + U (7.6)
D Hдисс + E Cl + U (7.6)
Ну, а вам останется только построить его графически еще раз.
Рассмотрим возможности цикла Борна – Габера на примере хлоридов (MeCl) и дихлоридов (MeCl2) металлов. Величина U рассчитывается на основе закона Гесса (с использованием старых единиц – ккал).

Какие же из хлоридов металлов более термодинамически устойчивы? В обоих случаях общей стадией является атомизация твердого металла с затратой
неизвестного нам, но одинакового количества энергии D H ат. Очевидно, не эта величина определяет стабильность обоих хлоридов. Ионизация до двухвалентного состояния требует значительно большего количества энергии, чем однократная ионизация атома. На стадии ионизации хлора в случае MeCl2 также требуется затратить вдвое больше энергии, чем для MeCl. Энергетически выгодна форма MeCl2, а не MeCl. Хотя реакции 1-4 для MeCl и дают выигрыш
242 ккал/моль по сравнению с теми же реакциями для MeCl2, это преимущество полностью теряется на стадии образования кристаллической решетки из ионов. Выигрыш за счет энергии решетки MeCl2 оказывается 877 ккал/моль, что с избытком покрывает энергетические расходы на первых стадиях цикла. Поэтому, если даже соединение MeCl в какой-то момент возникает, то затем самопроизвольно по реакции диспропорционирования
2MeCl (тв.) = MeCl2 (тв.) + Me (тв.)
переходит в дихлорид. Тепловой эффект такого процесса будет равен
D H = –553 – D H ат ккал/моль, т.е. очень большой величине, как раз и определяющей самопроизвольное течение реакции. Таким образом, можно без преувеличения сказать, что величина энергии кристаллической решетки определяет химическую или валентную форму ионного соединения.
Энергия кристаллической решетки в рядах однотипных соединений определяет также ряд свойств физико-химического характера, например температуру плавления и твердость.
Таблица 6.3.
Некоторые свойства галогенидов натрия.
| Энергия решетки, ккал/моль | Температура плавления, °С | Твердость, ед. Мооса * | |
| NaF | 3,25 | ||
| NaCl | 2,5 | ||
| NaBr | 2,25 | ||
| NaI | 2,0 |
* За 10 принимается твердость алмаза, за 1 – твердость талька.
Видно, что U и свойства находится в прямой зависимости от радиуса иона. Вам остается графически построить оба цикла и по справочным данным оценить энергетические параметры для хлоридов магния, кальция, бария.
§ 4. Второе начало (второй закон) термодинамики. Энтропия. Выделение тепловой энергии в ходе реакции способствует тому, чтобы она протекала самопроизвольно, т.е. без постороннего вмешательства. Однако имеются и другие самопроизвольные процессы, при которых теплота равна нулю (например, расширение газа в пустоту) или даже поглощается (например, растворение нитрата аммония в воде). Это означает, что помимо энергетического фактора на возможность протекания процессов влияет какой-то другой фактор.
Он называется энтропийным фактором или изменением энтропии. Энтропия S является функцией состояния и определяется степенью беспорядка в системе. Опыт, в том числе повседневный, свидетельствует о том, что беспорядок возникает самопроизвольно, а чтобы привести что-нибудь в упорядоченное состояние, нужно затратить энергию. Это утверждение – одна из формулировок второго начала термодинамики.
Существуют и другие формулировки, например, такая: Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (Клаузиус, 1850). Брусок, нагретый с одного конца, со временем принимает одинаковую температуру по всей длине. Однако никогда не наблюдается обратный процесс – равномерно нагретый брусок самопроизвольно не становится более теплым с одного конца и более холодным с другого. Другими словами, процесс теплопроводности необратим. Чтобы отнять тепло у более холодного тела, нужно затратить энергию, например, бытовой холодильник расходует для этого электрическую энергию.
Рассмотрим сосуд, разделенный перегородкой на две части, заполненные различными газами. Если убрать перегородку, то газы перемешаются и никогда не разделятся самопроизвольно снова. Добавим каплю чернил в сосуд с водой. Чернила распределятся по всему объему воды и никогда не соберутся
самопроизвольно в одну каплю. В обоих случаях самопроизвольно протекающие процессы сопровождаются увеличением беспорядка, т.е. возрастанием энтропии (D S > 0). Если мы рассматриваем изолированную систему, внутренняя энергия которой измениться не может, то самопроизвольность процесса в ней определяется только изменением энтропии: В изолированной системе самопроизвольно идут только процессы, сопровождающиеся возрастанием энтропии (Больцман, 1896). Это также одна из формулировок второго начала термодинамики. Наглядно проявление энтропийного фактора можно увидеть в фазовых переходах лед–вода, вода–пар, протекающие при постоянной температуре. Как известно при этом происходит поглощение (ледоход – похолодание) и выделение тепла (ледостав – потепление) так, что
D H Г = D S×T (7.7),
где D H Г – «скрытая» теплота фазового перехода. В фазовых переходах лед–вода–пар – D S л< D S в< D S п, т.е. энтропия возрастает при переходе от твердого тела к жидкости и от жидкости к газу, а ее величина тем больше, чем беспорядочнее движутся молекулы. Таким образом, энтропия отражает структурные отличия одного и того же химического элемента, молекулы, вещества. Например, для той же воды H2O – кристалл, жидкость, пар; для углерода – графит, алмаз, как аллотропные модификации и т.д.
Абсолютное значение энтропии можно оценить с использованием третьего начала термодинамики (постулата Планка), которое утверждает, что энтропия идеального кристалла при 0 К равна нулю lim D S =0 (при T®0).
Единицей измерения энтропии в системе СИ является Дж/К×моль. При этом понятно, что абсолютный нуль температуры недостижим (следствие из второго закона термодинамики), но он имеет важное значение в определении температуры – шкалы Кельвина.
Кроме того, есть еще одна функция состояния вещества – теплоемкость
D С = D H /D T, (7.8)
которая имеет такую же размерность, что и энтропия, но означает способность того или иного вещества отдавать (принимать) тепло при изменении температуры. Например, при изменении температуры на 100°С сталь быстрее нагреется и остывает соответственно, чем кирпич, поэтому печки кладут из кирпича. Величины теплоемкости удельные или молярные табулированы в справочниках обычно для изобарных условий – cp.
Стандартные абсолютные энтропии S °298 образования некоторых веществ приведены в справочной литературе. Обратите внимание, что в отличии от D Hf простые вещества имеют значения S °298 > 0, т.к. их атомы и молекулы также находятся в беспорядочном тепловом движении. Чтобы найти изменение энтропии в реакции, можно также применить следствие закона Гесса:
D S (реакции) = S S (продуктов) – S S (реагентов) (7.9)
D S > 0 согласно второму началу термодинамики благоприятствует протеканию реакции, D S < 0 — препятствует.
Качественно можно оценить знак D S реакции по агрегатным состояниям реагентов и продуктов. D S > 0 для плавления твердых тел и испарения жидкостей, растворения кристаллов, расширения газов, химических реакций, приводящих к увеличению числа молекул, особенно молекул в газообразном состоянии. D S < 0 для сжатия и конденсации газов, затвердевания жидкостей, реакций, сопровождающихся уменьшением числа молекул.
Пользуясь справочными данными, рассчитаем D S °298 реакции (а).
4Al (тв.) + 3PbO2 (тв.) = 2Al2O3 (тв.) + 3Pb (тв.)
S °298 4×28,32 3×76,6 2×50,99 3×64,89
D S °298 = 2×50,99+3×64,89–4×28,32–3×76,6 = –46,4 Дж/К.
Таким образом, энтропийный фактор препятствует протеканию этой реакции, а энергетический фактор (см. выше) – благоприятствует.
Идет ли реакция на самом деле? Чтобы ответить на этот вопрос, нужно одновременно рассмотреть оба фактора: энтальпийный и энтропийный.
§ 5. Свободная энергия Гиббса. Критерии самопроизвольности протекания химических реакций. Одновременный учет энергетического и энтропийного факторов приводит к понятию еще одной полной функции состояния – свободной энергии. Если измерения проводятся при постоянном давлении, то величина называется свободной энергией Гиббса (в старой химической литературе – изобарно-изотермическим потенциалом) и обозначается D G.
Свободная энергия Гиббса связана с энтальпией и энтропией соотношением:
D G = D H – T D S (7.10)
где T – температура в кельвинах. Изменение свободной энергии Гиббса в ходе реакции образования 1 моля вещества из простых веществ в стандартных состояниях называется свободной энергией образования Δ G ° и обычно выражается в кДж/моль. Свободные энергии образования простых веществ приняты равными нулю. Чтобы найти изменение свободной энергии Гиббса в ходе реакции, нужно от суммы свободных энергий образования продуктов отнять сумму свободных энергий образования реагентов с учетом стехиометрических коэффициентов:
D G (реакции) = SD G (продуктов) – SD G (реагентов) (7.11)
Самопроизвольным реакциям соответствует D G < 0. Если D G > 0, то реакция при данных условиях невозможна. Рассмотрим реакцию (a)
4Al (тв.) + 3PbO2 (тв.) = 2Al2O3 (тв.) + 3Pb (тв.)
Δ G °298 0 3×(–219,0) 2×(–1576,5) 0
Δ G °298 = 2×(–1576,5)–3×(–219,0) = –2496 кДж.
Существует и другой способ расчета D G реакции. Выше мы нашли значения Δ H и Δ S, тогда D G = D H – T D S
D G °298 = –2509,8 кДж – 298,15 К×(–0,0464 кДж/К) = –2496 кДж.
Таким образом, реакция (1) при стандартных условиях протекает самопроизвольно. Знак Δ G показывает возможность осуществления реакции только в условиях, для которых проводились вычисления. Для более глубокого анализа необходимо раздельное рассмотрение энергетического и энтропийного факторов. Имеется четыре возможных случая:
Таблица 7.3.
Определение возможности протекания химической реакции
| Критерии | Возможность |
| D H < 0, D S > 0 | Оба фактора благоприятствуют реакции. Как правило, такие реакции протекают быстро и полностью. |
| D H < 0, D S < 0 | Энергетический фактор благоприятствует реакции, энтропийный препятствует. Реакция возможна при низких температурах. |
| D H > 0, D S > 0 | Энергетический фактор препятствует реакции, энтропийный благоприятствует. Реакция возможна при высоких температурах. |
| D H > 0, D S < 0 | Оба фактора препятствуют реакции. Такая реакция невозможна. |
Если при стандартных условиях D G реакции > 0, но энергетический и энтропийный факторы направлены противоположно, то можно рассчитать, при каких условиях реакция станет возможной. D H и D S химической реакции сами по себе слабо зависят от температуры, если какие-нибудь из реагентов или продуктов не испытывают фазовых переходов. Однако в энтропийный фактор помимо D S входит также и абсолютная температура T. Таким образом, с повышением температуры роль энтропийного фактора повышается, и при температуре выше T» D H /D S реакция начинает идти в обратном направлении.
Если D G = 0, то система находится в состоянии термодинамического равновесия, т.е. D G – термодинамический критерий химического равновесия реакций (смотри вышеприведенные фазовые переходы воды).
Итак, анализируя функции состояния системы – энтальпию, энтропию и свободную энергию Гиббса – и их изменение в ходе химической реакции, можно определить, будет ли данная реакция происходить самопроизвольно, и тем самым ответить на вопросы, поставленные в начале этой лекции.
Более полно термодинамика отражена в курсе физической химии, а с прикладными ее аспектами вы ознакомитесь в курсах теплотехники и др.
Лекция 9
Химическая кинетика И катализ.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Как протекают реакции во времени? Закономерностями протекания процессов во времени занимается химическая кинетика. Для управления химическими процессами необходимо знание скоростей химических реакций и факторов, влияющих на скорость.
§ 1. Скорость химической реакции. Основным понятием химической кинетики является скорость реакции. Скоростью химической реакции называют изменение количества реагирующего вещества или образующегося продукта в единице объема за единицу времени.
Для гомогенной (однофазной) системы реакционным пространством служит объем, и скорость v может быть выражена:
 ;
;  ;
; 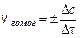 ;
;  (9.1)
(9.1)
где D n – изменение количества вещества; t – время; D c – изменение концентрации. В кинетике под реагентами понимают исходные вещества, а образующиеся в ходе реакции вещества – продукты.
Изменение концентрации веществ показаны на рис. 9.1. Видно, что u для исходных веществ имеет знак (–) минус.
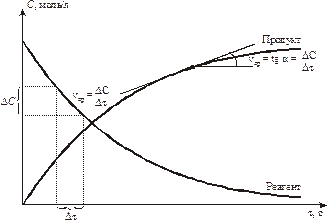
Рис. 9.1. Изменение концентраций реагентов и продуктов при химическом взаимодействии.
Для гетерогенных систем (различные фазы) реакции протекают на поверхности раздела фаз, и скорость определяется количеством вещества, вступившего
в реакцию или получившегося в результате реакции (D n) за единицу времени (Dt) на единице поверхности раздела (S):
 ;
;  ;
;  (9.2)
(9.2)
Основной закон химической кинетики – закон действующих масс (ЗДМ), высказанный в 1865 г. М.Н. Бекетовым и уточненный норвежскими химиками Гульдбергом и Вааге. Зависимость скорости химической реакции от концентрации выражается законом действующих масс: скорость простой химической реакции прямо пропорциональна концентрации реагирующих веществ, взятых в степенях, равных стехиометрическим коэффициентам в уравнении реакции (aA+bB=dD), или в математическом виде:
 (9.3)
(9.3)
где k – константа скорости химической реакции, равная скорости химической реакции при концентрациях реагирующих веществ 1 моль/л.; a и b – частные порядки реакции, С – концентрации.
Например, для реакции 2А+В=А2В скорость определится следующим
образом:
v = k CA 2 CB (9.4)
Константа скорости не зависит от концентрации веществ, а зависит от температуры. Выше указанное отношение (9.3) справедливо только для гомогенных реакций. Для гетерогенных процессов концентрация вещества в твердой фазе не меняется, поэтому скорость определяется концентрацией газов или растворенных веществ. Так, для реакции С+О2=СО2
 (9.5)
(9.5)
Обычно концентрацию газов заменяют парциальным давлением газа PO 2. Численное значение k при этом станет другим.
Классификация химических реакций. В химической кинетике реакции классифицируют по I. молекулярности и порядку реакции; II. по механизму протекания.
I. 1) Молекулярность определяется числом молекул, участвующим в элементарном химическом акте:
Н2 = 2Н – мономолекулярная;
CН3COOC2H5 + H2O = CН3COOH + C2Н5OH – бимолекулярная;
2NO + Cl2 = 2NOCl – тримолекулярная.
Реакции с молекулярностью большей трех не встречаются, т.к. вероятность столкновения сразу четырех и более молекул очень мала.
2) Порядок реакции – это сумма показателей степеней при концентрациях веществ в уравнении закона действующих масс. Так, реакции (9.5) – первого порядка, реакция (9.4) – третьего порядка. Иногда указывают частный порядок реакции по веществу – это степень, в которую возводится концентрация этого вещества.
II. 1) Параллельные реакции. Практически выгодным является получение перхлората калия, который является одним из компонентов ракетного топлива, поэтому изучение скорости и факторов влияющих на скорость химических реакций позволяет управлять параллельными реакциями и достигнуть v 1 < v 2.
2KOH + Cl2  KClO + KCl, 6KOH + Cl2
KClO + KCl, 6KOH + Cl2  KClO + 5KCl
KClO + 5KCl
2) Последовательные реакции А  В
В  С
С  D. Чтобы управлять процессом, необходимо выявить стадию, у которой скорость реакции минимальна, то есть скорость реакции, которая является лимитирующей для всего процесса. Затем, подбирая условия реакции, увеличивать скорость лимитирующей стадии, тем самым будет увеличиваться скорость всего процесса.
D. Чтобы управлять процессом, необходимо выявить стадию, у которой скорость реакции минимальна, то есть скорость реакции, которая является лимитирующей для всего процесса. Затем, подбирая условия реакции, увеличивать скорость лимитирующей стадии, тем самым будет увеличиваться скорость всего процесса.
3) Сопряженные реакции. Одна реакция идет только в том случае, если идет вторая.
§ 2. Уравнение Аррениуса. Скорость химической реакции зависит от температуры. При повышении температуры скорость большинства химической реакций увеличивается. Вант-Гофф показал, что при повышении температуры на 10 град., скорость реакции увеличивается в 2-4 раза (правило Вант-Гоффа):
 (9.6)
(9.6)
Температурный коэффициент реакции g равен отношению скоростей реакции, когда Т2–Т1=10 град. и показывает, во сколько раз увеличивается скорость реакции при повышении температуры на 10 град. Но уравнение (9.6) лишь приблизительно оценивает зависимость скорости реакции и константы скорости от температуры. Функциональную зависимость константы скорости реакции от температуры установил Аррениус (9.7).
 (9.7)
(9.7)
где k 0 – начальная скорость или предэкспоненциальный множитель – А. Графически величину Е а по Аррениусу можно представить на рис. 9.2.
В логарифмической форме это уравнение для констант скоростей преобразуется:
ln k = – Ea / RT + ln k 0 (9.8)
Видно, что зависимость константы скорости реакции от температуры линейна, следовательно можно определить энергию активации по тангенсу угла наклона прямой и k 0 – по отрезку, отсекаемому прямой по оси ординат, когда 1/Т→0. Энергию активации легко рассчитать, если известны константы скорости при разных температурах.
Все молекулы, запас энергии, которых не ниже энергетического барьера называются активными и они находятся в состоянии активированного комплекса. В состоянии активированного комплекса нет уже исходных веществ, но и еще нет продуктов реакции (старые связи еще не до конца разорвались, а новые
не образовались). Энергия такой системы максимальна, а значит, активированный комплекс неустойчив.
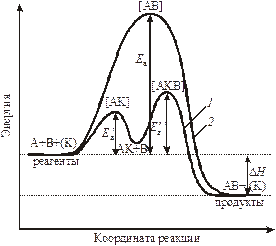
Рис. 9.2. Энергетический профиль реакции: 1 – в присутствии катализатора; 2 – без катализатора. Под координатой реакции понимается многопараметровая функция, зависящая от времени, пространственных координат молекул реагентов и др.
Разница в энергиях между исходным и переходным состоянием равна энергии активации. То есть, активные молекулы должны обладать энергией активации для осуществления взаимодействия для того, чтобы произошло ослабление связей в исходных веществах, для преодоления отталкивания между электронами в сближающихся молекулах, которое мешает их столкновению. Следовательно, энергия активации является одним из параметров, характеризующих скорость процесса. Чем больше энергия активации, тем меньше скорость процесса. Если Еа больше 1000 кДж/моль, то реакция не протекает при комнатной температуре, такие реакции идут при особых условиях, высоких Т и Р. Энергия активации в первую очередь зависит от природы реагирующих частиц. Существуют реакции, у которых Еакт = 0 – это туннельные реакции, протекающие, как правило, при низких температурах.
§ 3. Влияние катализаторов на скорость химической реакции. Катализаторами называются вещества, увеличивающие скорость реакции, но не расходующиеся в результате ее протекания. Катализаторы обычно участвуют в образовании промежуточных соединений, но в конце реакции полностью регенерируются. Наряду с катализаторами существуют ингибиторы, замедляющие скорость реакции. Катализ – наиболее эффективный метод интенсификации промышленных химических процессов. С точки зрения закона Аррениуса катализаторы (К) снижают энергетический барьер, а ингибиторы увеличивают (рис. 9.2).
1) Катализ применим только тогда, когда свободная энергия Гиббса данной реакции отрицательна (DG<0).
2) В присутствии катализатора изменяется механизм химической реакции, она протекает через новые стадии, характеризующиеся небольшими значениями Еа.
3) При катализе не изменяется тепловой эффект реакции.
4) Если реакция не обратима, то катализатор не влияет на положение равновесия.
5) Катализаторы обычно действуют избирательно, селективно. Одним из универсальных катализаторов является вода.
Активность того или иного катализатора зависит от многих факторов. Активность катализатора может быть повышена специальными добавками – промоторами. Если катализатор и реагирующие вещества образуют одну фазу, то катализ называют гомогенным, если две фазы – гетерогенным. Для объяснения гомогенного катализа используют теорию промежуточных соединений. Согласно этой теории катализатор взаимодействует с одним из исходных веществ с образованием промежуточных соединений, при этом понижается энергия активации и растет скорость реакции. А+В=AB; А+К=[АК]; [АК]+В=AB+К.
Для своего прохождения реакция должна преодолеть «энергетический барьер» – энергию активации и чем меньше барьер, тем больше скорость реакции. Таким образом, скорость реакции определяется числом активных молекул и величиной энергии активации, последняя изменяется в пределах 40-350 кДж.
§ 4. Химическое равновесие. Химические реакции бывают необратимые (односторонние) и обратимые (двухсторонние) или равновесные. Необратимые реакции протекают только в одном направлении до полного превращения хотя бы одного из реагирующих веществ. Примером необратимой реакции может служить реакция разложения бертолетовой соли:
2KClO3 = 2KCl + 3O2
Обратимые реакции могут протекать как в прямом, так и в обратном направлении, в связи с этим ни одно из реагирующих веществ не расходуется полностью. Так, например, следуя рис. 9.1, в состоянии равновесия имеет место определенное количество как реагента, так и продукта. Например, реакция синтеза аммиака является обратимой:
3Н2 + N2 ⇄ 2NН3
Она может протекать как в сторону образования аммиака (прямой процесс), так и в сторону реагентов – молекулярного азота и водорода (обратный процесс). Знак обратимости реакции – стрелки с противоположными направлениями: ⇄.
Выразим для обратимого процесса две скорости прямой ( ) и обратной реакции (
) и обратной реакции ( ) по закону действующих масс:
) по закону действующих масс:
 (9.9)
(9.9)
 (9.10)
(9.10)
Когда скорости прямой и обратной реакций становятся равными, наступает химическое равновесие. Комбинируя уравнения 9.9, 9.10, получим:
 (9.11)
(9.11)
Это уравнение отвечает кинетическому условию равновесия. Химическое равновесие называют динамическим. Этим подчеркивается, что при равновесии протекают как прямая, так и обратная реакции, но их скорости равны, а устанавливается оно с течением времени.
Кравн – константа равновесия является количественной мерой, характеризующей реакцию в состоянии химического равновесия. Закон действующих масс для обратимого процесса можно сформулировать: В состоянии химического равновесия отношение произведения концентраций продуктов реакции к произведению концентраций исходных веществ есть величина постоянная. При этом концентрация каждого вещества берется в степени его стехиометрического коэффициента в уравнении реакции. Значения некоторых Кравн приведены в «Практикуме».
Система находится в состоянии равновесия до тех пор, пока внешние условия сохраняются постоянными. Если же условия изменятся, то система выйдет из равновесия. При этом скорости прямого и обратного процессов изменяются неодинаково, и будет протекать преимущественно только один процесс (прямой или обратный), т.е. произошло смещение равновесия. Оно происходит под действием таких факторов: изменение концентрации веществ, температуры, давления и подчиняется универсальному принципу Ле-Шателье: Всякое внешнее воздействие на равновесную химическую систему вызывает в ней процесс, приводящий к уменьшению эффекта внешнего воздействия, который часто называют «третьим законом Ньютона в химии» и имеющий универсальный характер в природе.
Влияние изменения концентрации веществ на смещение равновесия. По принципу Ле-Шателье увеличение концентрации исходных веществ сместит равновесие в сторону той реакции, при которой происходит уменьшение количества исходных веществ, т.е. в сторону превращения исходных веществ в продукт реакции.
Наоборот, увеличение концентрации продуктов реакции сместит равновесие в сторону образования исходных веществ. Уменьшение же концентрации продуктов реакции сместит равновесие в сторону образования продуктов реакции и концентрация их возрастет.
Обобщая, можно сделать вывод, что при увеличении концентрации какого-либо из веществ равновесие смещается в сторону расхода этого вещества;
при уменьшении концентрации какого-либо вещества равновесие смещается в сторону образования этого вещества.
Равновесие подавляющего большинства реакций смещается при изменении температуры. Фактором, определяющим направление смещения равновесия, является знак теплового эффекта реакции. Из принципа Ле-Шателье следует, что при повышении температуры равновесие смещается в сторону эндотермической реакции, а при охлаждении – в сторону экзотермической реакции.
В рассматриваемом случае синтез аммиака представляет собой экзотермический процесс: D H =–92 кДж/моль. Поэтому при повышении температуры равновесие смещается в сторону обратной реакции, разложения аммиака.
В соответствии с принципом Ле-Шателье при увеличении давления в системе путем сжатия равновесие сдвигается в сторону уменьшения числа молей газа; при уменьшении давления равновесие сдвигается в сторону возрастания числа молей газов.
Например, при синтезе аммиака при протекании прямого процесса из четырех молей газа образуется два моля газа, значит число молей газа уменьшается в два раза, что приводит к уменьшению давления в сосуде. При обратном процессе число молей газа наоборот возрастает, следовательно, возрастает и давление. Отсюда, вывод: синтез аммиака нужно вести при высоких давлениях. В том случае, когда реакция протекает без изменения числа молей газа, равновесие при изменении давления не нарушается. Напомним, что термодинамическим критерием химического равновесия является DG=0, что особенно наглядно проявляется при фазовых переходах.
Термодинамические и кинетические критерии химического равновесия связаны уравнением:
D G = – RT ln Kравн (9.12).
Из уравнения видно, что высоким отрицательным значениям DG отвечает большое значение константы равновесия (Kp), это значит, что в равновесной смеси преобладают продукты реакции. Если же DG имеет большое положительное значение (Kp), то в равновесной смеси преобладают исходные вещества. Уравнения (9.9) позволяют по величине DG вычислить константу равновесия (Кравн), а затем и равновесные концентрации или парциальные давления реагентов.
Таким образом, количественно химическое равновесие оценивается термодинамическим критерием (DG) и кинетическим критерием (равенство скоростей прямой и обратной реакций, Kp).
Лекция 10
Растворы
§ 1. Определение растворов. Растворимость. Способы выражения концентрации. Для того чтобы между двумя веществами произошла химическая реакция, их молекулы должны вступить в контакт друг с другом. Так, если измельчить твердые вещества в порошок, то реакции между ними ускорятся во много раз. Растворяя эти вещества, мы дробим их до наименьших возможных частиц – молекул или ионов, поэтому большинство химических реакций оказывается выгодным проводить в растворах. Реакции, протекающие в растворах, имеют важное значение для биохимии, химической технологии и т.д. Современное учение о растворах создавалось на протяжении примерно двухсот лет, в него внесли вклад такие знаменитые ученые, как М. Фарадей, Гельмгольц, Д.И. Менделеев, Аррениус, Вант-Гофф, Оствальд, Каблуков и другие. Современное определение понятия раствор следующее:
Раствором называется гомогенная многокомпонентная химическая система, состав которой в определенных пределах может варьироваться (быть переменным) без качественного изменения свойств.
Это определение требует некоторых комментариев. Гомогенная – значит, ее свойства однородны по всему объему, т.е. отсутствуют границы раздела фаз; многокомпонентная – означает совокупность нескольких веществ: растворителя и одного или нескольких растворенных веществ – компонентов. Химическая система переменного состава означает взаимодействие растворителя и компонентов с образованием химических соединений переменного состава.
Химическое взаимодействие растворителя с компонентами называется сольватацией, а в случае растворителя воды – гидратацией. Процесс этот сопровождается поглощением или выделением тепла, как и в других химических реакциях. Образующиеся сольваты и гидраты в растворе в зависимости от концентрации, температуры, давления и других факторов имеют переменный состав в отличии от исходных реагентов: растворителя и компонентов. Например, H2O и C2H5OH – соединения постоянного состава образуют сольваты {(H2O)x× (C2H5OH)y}, где x и y – целые числа (1,2,3) – соединения переменного состава. Растворы как бы занимают промежуточное положение между смесями и химическими соединениями. Растворы обладают определенной структурой, особенно для ближайшего окружения сольватов.
Важной количественной характеристикой растворов являются концентрация и растворимость. Под концентрацией понимается количество растворенного вещества в объеме раствора (растворителя). Под растворимостью понимается максимально возможное количество растворенного вещества в объеме (массе) растворителя до появления осадка (гетерогенная система, и есть граница раздела фаз). Естественно, они зависят от температуры и других внешних факторов. Растворы могут быть твердыми, жидкими и газообразными. Они также классифицируются на растворы неэлектролитов и электролитов, о которых будет идти речь в следующих лекциях.
Как правило, растворимость твердых веществ повышается с ростом температуры (хотя есть исключения) и мало зависит от изменения внешнего давления. Растворимость газов также варьирует в широких пределах (от 0,2 объема на
1 объем воды у гелия до 800 объемов у аммиака), однако понижается с ростом температуры и повышается с ростом парциального давления газа.
В случае ограниченной растворимости можно выделить растворы ненасыщенные, содержание растворенного вещества в которых меньше, чем максимально возможное при данных условиях; насыщенные, в которых данное вещество при данных условиях больше не растворяется, и пересыщенные, содержание растворенного вещества в которых больше, чем в насыщенном растворе при данных условиях (пересыщенный раствор можно получить, например, быстрым охлаждением раствора вещества, растворимость которого значительно повышается с ростом температуры). Пересыщенные растворы метастабильны, т.е. способны под действием внешних факторов, а иногда и самопроизвольно, переходить в устойчивое состояние (насыщенный раствор + избыток растворенного вещества в отдельной фазе).
Способы выражения концентрации растворов даны в «Практикуме». Значения растворимостей различных веществ в различных растворителях табулированы в многочисленных химических справочниках.
§ 2. Термодинамические свойства растворов. Для растворов характерны несколько законов. К ним относятся: понижение давления пара растворителя, повышение температуры кипения и понижение температуры замерзания раствора, осмотическое давление и другие, связывающие концентрацию, растворимость с физическими параметрами раствора, как химической системы.
Величина относительного понижения давления пара (депрессии) над раствором по сравнению с чистым растворителем пропорциональна концентрации растворенного вещества (закон Рауля):
 , (10.1)
, (10.1)
где P 0 – давление пара над чистым растворителем, P — давление пара над раствором, N 2 – мольная доля растворенного вещества.
Физическую природу этого явления можно пояснить следующим образом. В замкнутой системе, состоящей из жидкого растворителя и паров над ним, при постоянных условиях устанавливается динамическое равновесие между жидкой и газообразной фазой: количество молекул, перешедших из газообразной фазы в жидкую за данный промежуток времени, равно количеству молекул, перешедших из жидкой фазы в газообразную. Первая величина зависит от содержания молекул растворителя в единице объема газовой фазы, вторая — от количества молекул растворителя на единицу поверхности раздела фаз. Добавление
нелетучего растворенного вещества уменьшает только вторую величину (часть поверхности занята молекулами растворенного вещества), поэтому положение равновесия должно сместиться в сторону уменьшения давления пара растворителя. Т.е. давление пара воды над морской водой меньше чем над пресной. У закона Рауля есть два следствия, связанные с кипением и замерзанием (отверждением) растворов по сравнению с растворителем.
Повышение температуры кипения растворов, по сравнению с растворителем называется эбулиоскопией, а математически выражается формулой:
D Tкип = KE × Cm, (10.2)
где KE – эбулиоскопическая постоянная для данного растворителя, Сm – моляльная концентрация. Аналогично для замерзания растворов – криоскопия и уравнения для температуры замерзания раствора по сравнению с чистым растворителем и имеет вид:
D Tзам = KE × Cm, (10.3)
где КК – криоскопическая постоянная. Методами эбулиоскопии и криоскопии можно, например, определить молекулярную массу неизвестного вещества. Как известно, если к g 1 г растворителя добавить g 2 г растворенного вещества, то моляльная концентрация будет равна:
 , (10.4)
, (10.4)
где M – молекулярная масса растворенного вещества.
Тогда из уравнений (10.2)-(10.4) следует, что
 или
или  (105)
(105)
Наглядно следствия из закона Рауля объясняются изменениями на диаграмме состояния воды и раствора (рис. 10.1).
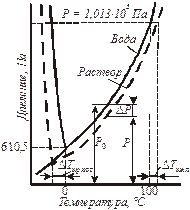
| Рис. 10.1. Фазовая диаграмма воды и раствора при постоянной концентрации. |
При пониженном по сравнению с чистым растворителем давлении паров над раствором «ветвь» граница раздела фаз понижается с увеличением концентрации растворенного вещества. При этом раствор кипит при большей температуре, чем растворитель, а замерзает при более низкой.
У эбулиоскопии и криоскопии очень много прикладных значений (посыпание солью снега зимой, охлаждающие смеси, высокотемпературные жидкости и т.д.).
У закона Рауля есть «родственник» – закон Генри: растворимость газов в жидкости пропорционально давлению:
C = k×p, (10.6)
где k – константа Генри, p – давление. Он наглядно иллюстрируется на примерах: сифон, газированная вода, наличием кислорода на больших водных глубинах, водолазная техника («кессонная болезнь») и т.д.
И наконец рассмотрим еще один закон – закон осмотического давления Вант-Гоффа.
P p = C×R×T, (10.7)
где P p – осмотическое давление, C – молярная концентрация, R – газовая постоянная, T – температура; напоминающий уравнение Клайперона – Менделеева, но связанный с явлением осмоса: давление растворителя над полупроницаемой мембраной выше, чем в растворе (с другой стороны мембраны). Не вдаваясь в суть явления осмоса, отметим, что под полупроницаемой понимается мембрана, проницаемая для молекул растворителя, но задерживающая молекулы растворенного вещества. Закон также имеет большое прикладное значение в природе и технике: рост растений, деревьев, очистка жидкостей и т.д.
Перечисленные термодинамические законы являются общими для всех растворов нелетучих веществ.
Лекция 11, 12
РАСТВОРЫ ЭЛЕКТРОЛИТОВ.
электролитическАЯ диссоциациЯ
Вещества, растворы (или расплавы) которых проводят электрический ток, называются электролитами, для которых Фарадей в начале XIX в. ввел понятие катион и анион и установил законы электролиза. Носителями электричества в растворе являются катионы и анионы, т.е. атомы и молекулы несущие положительный и отрицательный заряд, по Фарадею возникающие в процессе прохождения электрического тока. Лишь спустя почти полвека великий Сванте Аррениус установил, что все как раз наоборот: ионы (катионы, анионы) образуются в растворах электролитов всегда вследствие электролитической диссоциации полярных молекул и ионных кристаллов.
§ 1. Основные положения теории электролитической диссоциации. При растворении солей, кислот и оснований в воде происходит диссоциация этих веществ с образованием электрически заряженных частиц – катионов и анионов; электрическая проводимость водных растворов солей, кислот и оснований пропорциональна общей концентрации ионов в растворе. Таким образом, ионы самопроизвольно, изначально существуют в растворе электролитов, так что в целом раствор электронейтрален, а при наложении разности потенциалов проводит электрический ток. Аррениус ввел представление об электролитической диссоциации для объяснения природы изотоническогоё коэффициента – i, эмпирически в веденного Вант-Гоффом для выполнения термодинамических законов растворов электролитов, т.е. для законов Рауля, эбулиоскопии, криоскопии, Вант-Гоффа (10.1-10.5) он предложил ввести изотонический коэффициент – множитель концентрации. Так что, например, для осмотического давления следует писать
p = iCRT, (11.1)
С введением изотонического коэффициента эффективная концентрация электролита увеличивалась. По Аррениусу она увеличивалась за счет диссоциации – распада молекулы на несколько ионов.
Аррениус ввел понятие – степень электролитической диссоциации (a) как отношение числа молекул, продиссоциированных на ионы к общему числу молекул в растворе. Она меняется от 0 до 1, или от 0 до 100%.
Вспомните слабые, сильные электролиты, теперь они характеризуются a, которая связана с изотоническим коэффициентом следующим соотношением:
 , (11.2)
, (11.2)
где i = 1 для растворов неэлектролитов, i > 1 для растворов электролитов. С уменьшением концентрации i увеличивается  ; k – целое число ионов в результате полной диссоциации, для бинарных электролитов (KCl, HCl) k = 2, для H3PO4: k =4, i <4 и т.д.
; k – целое число ионов в результате полной диссоциации, для бинарных электролитов (KCl, HCl) k = 2, для H3PO4: k =4, i <4 и т.д.
Таким образом, в растворах электролитов имеет место гидратация и сольватация (Менделеев) и электролитическая диссоциация (Аррениус) как два единых процесса растворения электролитов в растворе («две стороны одной медали»), что и ввел в теорию и практику Каблуков.
Электролитическая диссоциация вызывается взаимодействием полярных молекул растворителя с частицами растворяемого вещества. Это взаимодействие приводит к поляризации связей. Происходит образование ионов за счет «ослабления» и разрыва связей в молекулах растворяемого вещества. Переход ионов в раствор сопровождается их гидратацией:

Рис. 11.1. Схема процессов гидратации и диссоциации полярной молекулы электролита типа HCl (разрыв ионогенной полярной ковалентной связи с ее переходом в ионную связь).
Кратко остановимся на водных растворах электролитов, основными участниками которых являются вода, кислоты, щелочи, соли и образуемые ими гидраты ионов (аквакомплексы), комплексные соединения.
Особенностью водных растворов электролитов является ион водорода (протон), имеющий малый размер (10–4 от размера атома), и образующий при гидратации ион гидроксония – Н3О+. Новая ковалентная связь образуется по донорно-акцепторному механизму за счет свободной электронной пары кислорода (донора) и вакантной орбитали протона (акцептора).
Характер ионов, образующихся при диссоциации различных электролитов, естественно, должен быть различным. В молекулах солей диссоциация всегда приводит к образованию катионов металла и анионов кислотного остатка. Кислотами являются электролиты, которые диссоциируют с образованием ионов Н+. Сильные кислоты (HCl, HBr, HI, HNO3, H2SO4) диссоциируют практически полностью, у слабых кислот диссоциирована лишь часть молекул. Основание определяют как электролит, диссоциирующий с образованием ионов ОН–. Сильные основания (NaOH, KOH) диссоциируют практически полностью, у слабых электролитов диссоциирована лишь некоторая доля молекул.
Существуют электролиты, которые могут диссоциировать как кислоты и как основания. Такие электролиты называются амфотерными электролитами (амфолитами). Амфотерность электролитов объясняется малым различием прочности связей Me–O и H–O. Примером амфотерного электролита может быть гидроксид цинка:
2H++ZnO22– ⇄ H++HZnO2– ⇄ Zn(OH)2 ⇄ZnOH++OH– ⇄Zn2++2OH–
При взаимодействии с азотной кислотой
Zn(OH)2 + 2HNO3 = Zn(NO3)2 + 2H2O
при взаимодействии с гидроксидом калия
Zn(OH)2 + 2KOH = K2ZnO2 + 2H2O
В растворах слабых электролитов процесс диссоциации протекает обратимо и, следовательно, к нему может быть применен закон действия масс, например:
CH3COOH ⇄ CH3COO–+ H+
Константа равновесия Kp будет равна:
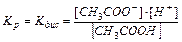 (11.3).
(11.3).
Константа равновесия для процесса диссоциации называется константой диссоциации Kдис.
Установлено, что многоосновные кислоты отщепляют ион водорода не сразу, а постепенно. Например,
1) H3PO4 ⇄ H++H2PO4– K1=7,11×10–3
2) H2PO4 ⇄ H++HPO42– K2=6,34×10–8
3) HPO4 ⇄ H++PO43– K3=1,26×10–12
Каждая ступень характеризуется своей константой диссоциации, но первая ступень идет легче, поэтому К1 больше следующей и т.д.
Константа диссоциации представляет собой важную характеристику слабых электролитов, так как указывает на прочность их молекул в данном растворе. Чем меньше константа диссоциации в данном растворителе, тем слабее диссоциирует электролит и тем устойчивее его молекулы.
Константа электролитической диссоциации зависит лишь от природы электролита и температуры. Между константой и степенью электролитической диссоциации существует количественная связь. Действительно, пусть в рассмотренном процессе общая концентрация растворенного вещества КА равна C, а степень диссоциации равна a. Тогда [ K +] = [ A –] = a× C и соответственно концентрация недиссоциированных частиц [ KA ] = (1–a)× C. Подставив эти значения в выражение для константы диссоциации, получим известный закон разбавления Оствальда:
 (11.4)
(11.4)
Это соотношение называется законом разбавления Оствальда. Для слабых электролитов, когда a <<1, Кдис ≈ a2 C. Отсюда
 или
или  , (11.5)
, (11.5)
где V =1/ C – разбавление. Из формулы следует, что при разбавлении раствора в 100 раз степень диссоциации возрастет в 10 раз.
Электропроводность растворов электролитов зависит от их концентраций в растворе. Величина, характеризующая данный раствор, называется удельной электропроводностью c
c = 1 / r (11.6)
где r– удельное электрическое сопротивление.
С разбавлением раствора она уменьшается, вследствие уменьшения концентрации, но в тоже время увеличивается степень диссоциации.
§ 2. Сильные электролиты. Активность. Согласно теории диссоциации, сильные электролиты практически полностью диссоциируют не только в разбавленных растворах, но и в растворах любой концентрации. Другими словами, в любых растворах сильных электролитов степень их диссоциации a =1 (100%).
Таким образом, считается, что в растворах сильных электролитов нет недиссоциированных молекул, поэтому понятие константы диссоциации к ним не применимо (знаменатель выражения вида (11.3) равен нулю).
При определенных условиях, например, когда растворитель обладает малой диэлектрической проницаемостью, создаются условия для электростатического взаимодействия сольватированных ионов противоположного знака. При этом последние подходят друг к другу на близкое расстояние и образуют так называемую ионную пару – сложный агрегат, состоящий из двух противоположно заряженных ионов, окруженных молекулами растворителя, в котором электрические заряды взаимно компенсированы.
При повышении концентрации раствора расстояния между ионами сокращаются, что усиливает межионное взаимодействие. Вследствие этого экспериментально определяемые свойства растворов сильных электролитов, зависящие от общего количества частиц в растворе, оказываются меньше рассчитанных в предположении полной диссоциации.
Чтобы можно было пользоваться простыми соотношениями идеальных растворов для описания поведения реальных растворов, Льюис (1907) ввел формальное представление об эффективной концентрации – активности. Активность связана с истинной концентрацией растворенного вещества соотношением
a = f × C, (11.7)
где a – активность, f – коэффициент активности, C – концентрация.
Активность выражается в тех же единицах, что и концентрация, поскольку коэффициент активности – величина безразмерная. Он характеризует степень отклонения свойств данного раствора от свойств идеального раствора. Для бесконечно разбавленных растворов электролитов, где практически отсутствует взаимодействие ионов, активность становится равной концентрации и коэффициент активности равен единице.
Так как коэффициенты активности учитывают также степень диссоциации электролита в растворе, их применяют и при описании свойств растворов слабых электролитов. Коэффициенты активности вычисляют по экспериментальным данным. Для этого измеряют какое-либо из свойств раствора (например, электропроводность, температуру кипения или замерзания) и определяют коэффициент активности как частное от деления экспериментально полученной величины на теоретически рассчитанную по законам идеальных растворов:
Таблица 11.1
Коэффициенты активности некоторых электролитов в растворах при 298 К
| Концентрация, | f ± для электролитов | ||||||
| NaCl | KCl | NaOH | KOH | HCl | H2SO4 | CaCl2 | |
| 0,001 0,01 0,1 0,5 1,0 2,0 5,0 | 0,965 0,874 0,778 0,681 0,657 0,668 0,874 | 0,966 0,901 0,769 0,651 0,607 0,576 — | 0,966 0,900 0,776 0,693 0,679 0,700 1,060 | 0,966 0,900 0,766 0,712 0,735 0,863 1,670 | 0,966 0,904 0,796 0,758 0,809 1,010 2,380 | 0,830 0,544 0,265 0,156 0,132 0,128 0,208 | 0,840 0,850 0,518 0,448 0,500 0,792 0,890 |
В области разбавленных растворов (ниже 0,1 моль/л) коэффициенты активности зависят главным образом от концентрации и заряда ионов, присутствующих в растворе, и мало зависят от природы растворенных веществ. Эта закономерность известна в теории растворов под названием «правила ионной силы», учитывающее электростатическое взаимодействие ионов и диполей. Согласно этому правилу ионы одинакового заряда независимо от их природы в разбавленных растворах с одинаковой ионной силой имеют равные коэффициенты активности. Ионной силой раствора (I) называется полусумма произведений концентрации всех ионов, на квадрат их заряда (z):
 (11.8)
(11.8)
Поиск по сайту: