Работа силы

Умножив обе части основного закона динамики для случая постоянной массы МТ – соотношение (1.2) скалярно на , получим:

или, учитывая, что ,

. (1.38)

Так как , то, взяв дифференциал от обеих частей, получим:

: .

Учтя, что масса постоянна, находим , и тогда соотношение (1.38) примет вид:

(1.39) или , (1.40)

где правые части соотношений (1.39) и (1.40) представляют собой

элементарную работу силы, действующей на МТ:

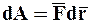. (1.41)

Выражения (1.39) или (1.40) представляют первую дифференциальную форму теоремы об изменении кинетической энергии МТ.

Теорема: Дифференциал кинетической энергии МТ равняется элементарной работе силы, действующей на МТ.

Поделив соотношения или (1.39) или (1.40) на dt, получим вторую дифференциальную форму теоремы об изменении кинетической энергии МТ:

, (1.42)

где является мощностью силы, действующей на МТ.

Теорема: Производная по времени от кинетической энергии МТ равняется мощности силы, приложенной к МТ.

Если рассмотреть конечное перемещение МТ из одного положения (1), где ее скорость равна 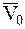в другое положение (2), где ее скорость равна , то, беря от обеих частей равенства (1.40) соответствующие интегралы, получим:

. (1.43)

Соотношение (1.43) выражает теорему об изменении кинетической энергии МТ в конечной (интегральной) форме.

Теорема: Изменение кинетической энергии МТ на конечном перемещении равняется работе силы, действующей на МТ на том же перемещении.

В соотношении (1.43) правая часть представляет собой работу силы, действующей на МТ на конечном перемещении:

. (1.44)

Учитывая, что , т. е. , преобразуем выражение (1.44)

. (1.45)

Рассмотрим частные случаи работы силы:

· Работа постоянной по модулю и направлению силы – , приложенной к МТ, движущейся прямолинейно.

Из соотношения (1.44) или (1.45) получим (рис. 12):

A=Fs cos a,

где a – угол между направлением движения МТ и силой.

Рис. 12

· Работа силы тяжести МТ при ее любом перемещении из одного положения в другое.

Выберем систему координат с осью Оz, направленной по вертикали вверх (рис. 13).

Рис. 13

Соотношение (1.44) для силы Р можно записать в виде:

. (1.46)

Тогда, проектируя силу тяжести на координатные оси, получим:

.

Следовательно, работа силы тяжести МТ на конечном участке траектории (от точки В₁ до точки В₂) равна

,

где Dh – разность высот положений МТ.

Из полученного соотношения видно, что работа силы тяжести МТ не зависит от формы траектории ее движения.

· Работа силы упругости (восстанавливающей силы), действующей на МТ.

Пусть МТ под действием силы упругости совершает прямолинейное движение вдоль оси Ох. При этом за начало координат берется точка О, соответствующая положению МТ при недеформированном состоянии пружины (рис. 14).

Учитывая, что сила упругости пропорциональна ее удлинению, получим:

,

где с – коэффициент жесткости пружины.

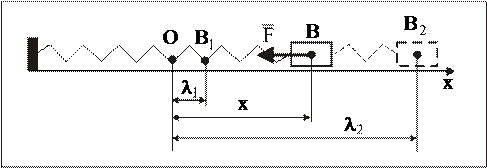
Рис. 14

Тогда соотношение (1.45) примет вид:

,

здесь l₁ и l₂ – удлинения пружины соответственно в первом и во втором положении МТ.

Поиск по сайту: