Параграф 4. Теорема об изменении количества движения МТ

Общие теоремы динамики МТ

Основной закон динамики (1.1) можно представить в виде:

(1.29)

Здесь 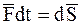– элементарный импульс силы, действующей на МТ.

Соотношение (1.29) выражает теорему об изменении количества движения МТ в дифференциальной форме.

Теорема: Дифференциал количества движения МТ равен элементарному импульсу силы, действующей на МТ.

Проинтегрировав соотношение (1.29) с учетом начальных условий: при t = 0 , получим эту теорему в конечной интегральной форме:

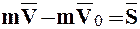. (1.30)

В (1.30) называется импульсом силы за конечный промежуток времени:

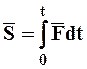. (1.31)

Теорема: Изменение количества движения МТ за конечный промежуток времени равно импульсу силы, действующей на МТ за тот же промежуток времени.

Проектируя на оси декартовой системы координат равенство (1.30), получим эту теорему в скалярной форме:

,

, (1.32)

,

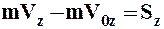где S_x, S_y, S_z – проекции импульса силы на оси декартовой системы координат.

Теорема: Изменение проекции количества движения МТ на какую-либо ось за конечный промежуток времени равно проекции на эту же ось импульса силы, действующей на МТ за тот же промежуток времени – соотношение (1.32).

Следствия: если =0, то , т. е. МТ движется таким образом, что ее скорость остается постоянной;

если F_x=0, то V_x = V_0х, т. е. МТ движется таким образом, что проекция ее скорости на ось х остается постоянной.

Первое из полученных соотношений находится в полном соответствии с первым законом динамики – законом инерции и подтверждает, что при отсутствии силы МТ движется равномерно и прямолинейно.

Поиск по сайту: