Дифракция на щели. Распределение интенсивности света при дифракции на щели

Распределение интенсивности света при дифракции на щели

В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.

Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать

пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([ , ]).

Расстояние r от щели определяется как:

Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биномиальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:

Видно, что 1/ r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.

Здесь мы введём некую константу 'C', которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.

В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:

Используя формулу Эйлера и её производную: и .

где ненормированная синкус функция определена как .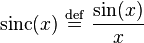

Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:

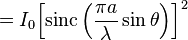
Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом, зонная пластинка действует как собирающая линза.

Также зонная пластинка представляет собой простейшую голограмму — голограмму точки.

Поиск по сайту: