 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 7
Вопрос 8. Эффект Керра.
Все физические воздействия, способные ориентировать структурные элементы первоначально изотропного вещества, могут вызывать возникновение искусственной оптической анизотропии. Электрооптический эффект – это появление оптической анизотропии первоначально изотропного вещества при помещении его в электрическое поле. Наблюдаются электрооптические эффекты двух типов: линейный и квадратичный. Эффект Керра, или квадратичный электрооптический эффект — явление изменения значения показателя преломления оптического материала пропорционально квадрату напряженности приложенного электрического поля. Эффект Керра был открыт в 1875 году шотландским физиком Джоном Керром. Эффект Керра, или квадратичный электрооптический эффект — явление изменения значения показателя преломления оптического материала пропорционально второй степени напряженности приложенного электрического поля. Эффект Керра является нелинейным оптическим эффектом, возникающим при распространении интенсивного света в кристаллах и стеклах, а также и в других средах, таких как газы. Его физическая природа связана с изменением поляризации вещества под воздействием внешнего постоянного или переменного электрического поля в среде, которая сама по себе изменяет свойства распространения света. Эффекта Керра – это эффект, при котором мгновенно происходит нелинейный отклик, который можно описать как изменение показателя преломления. В частности, показатель преломления для высокой интенсивность света изменяется в соответствии с формулой
∆n=n2·I,
где n2 нелинейный показатель, I - оптическая интенсивность. Значение n2 для различных сред может быть измерено, например, методом Z-сканирования.
Обратите внимание, что в дополнение к эффекту Керра (чисто электронной нелинейности), эффект электрострикции также может внести значительный вклад в значение нелинейного показателя. Электрическое поле вызывает изменения плотности света (акустических волн), которые сами по себе влияют на показатель преломления через фотоупругий эффект. Этот механизм, однако, происходит за гораздо больший промежуток времени и, таким образом, относится только к относительно медленным модуляциям мощности, но не для сверхкоротких импульсов.
Вопрос 9. Поляризация при отражении и преломлении света на границе раздела двух диэлектриков. Закон Брюстера
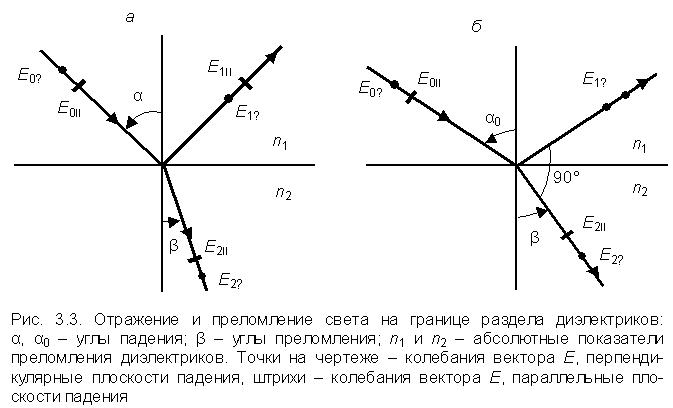
Наиболее простой способ получения линейно-поляризованного света из естественного основан на его отражении от границы раздела двух диэлектриков. На рис. 3.3 изображены в плоскости падения падающий E 0, отраженный E 1 и преломленный E 2 лучи света на границе раздела диэлектриков. Все возможные направления вектора  (рис. 3.3) можно разложить на два взаимно-перпендикулярных направления: параллельное
(рис. 3.3) можно разложить на два взаимно-перпендикулярных направления: параллельное  0II и перпендикулярное
0II и перпендикулярное  0┴ плоскости падения.
0┴ плоскости падения.
Решения уравнений Максвелла для электромагнитного поля на границе раздела двух диэлектриков (формулы Френеля) позволяют определить в отраженном и преломленном лучах амплитуды светового вектора  для двух различных поляризаций. Формулы Френеля для отраженного света имеют вид:
для двух различных поляризаций. Формулы Френеля для отраженного света имеют вид:
E 1II  ;
;
 ,
,
где a и b – углы падения и преломления соответственно. Из этих формул видно, что только при нормальном падении и близком к нему (a→0) компоненты  0II и Е 0┴ равны, т. е. отраженный свет остается неполяризованным. При других углах падения составляющая Е 1┴, перпендикулярная плоскости падения, оказывается больше параллельной составляющей
0II и Е 0┴ равны, т. е. отраженный свет остается неполяризованным. При других углах падения составляющая Е 1┴, перпендикулярная плоскости падения, оказывается больше параллельной составляющей  1II, так как sin(a+b) < tg(a+b). То есть отраженный свет при >0 является частично поляризованным.
1II, так как sin(a+b) < tg(a+b). То есть отраженный свет при >0 является частично поляризованным.
При выполнении равенства a0 + b = 90° (рис. 3.3, б; a = a0) параллельная компонента  1II обращается в нуль, и отраженный свет становится полностью линейно-поляризованным в плоскости, перпендикулярной плоскости падения.
1II обращается в нуль, и отраженный свет становится полностью линейно-поляризованным в плоскости, перпендикулярной плоскости падения.
Используя закон Снеллиуса
 ,
,
где n 21– относительный показатель преломления, для случая a0 + b = 90° можно получить соотношение, известное как закон Брюстера
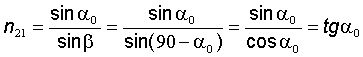 .
.
Угол a0, соответствующий такому направлению падающего луча, при котором отраженный луч полностью поляризован, называют углом полной поляризации или углом Брюстера.
Закон Брюстера формулируется так: тангенс угла полной поляризации равен относительному показателю преломления отражающего диэлектрика.
Так как в отраженном свете компоненты  1II и Е 1┴ не равны друг другу, то и в преломленном свете будет выполняться неравенство
1II и Е 1┴ не равны друг другу, то и в преломленном свете будет выполняться неравенство  1II > Е 1┴, т. е. преломленный свет будет частично поляризован. Максимальная, но неполная поляризация для преломленного луча будет наблюдаться также при падении естественного света под углом Брюстера.
1II > Е 1┴, т. е. преломленный свет будет частично поляризован. Максимальная, но неполная поляризация для преломленного луча будет наблюдаться также при падении естественного света под углом Брюстера.
Так как интенсивность света пропорциональна квадрату амплитуды светового вектора I ~ E 2, то формулы Френеля позволяют рассчитать зависимость интенсивности отраженного света от угла падения. Примерный вид этих зависимостей для двух поляризаций падающего излучения представлен на рис. 3.4.

Поляризаторы, основанные на преломлении света, состоят из ряда пластин («стопа Столетова»). Выходящий из стопы свет линейно-поляризован. Для получения максимальной степени поляризации с помощью стопы свет направляют на нее под углом Брюстера. Оптимальное количество пластин в стопе зависит от их показателя преломления: чем больше показатель преломления, тем меньше требуется пластин.
Отражающие поляризаторы представляют собой пластинки из диэлектрика с плоской поверхностью, полированной до зеркального блеска, на которые направляют свет под углом Брюстера. Эти зеркала делают из стекол, непрозрачных для данной области спектра, из германия и некоторых других материалов.
Вопрос 10. Волны от разных источников могут накладываться друг на друга. Это согласно принципу суперпозиции может привести к интерференции, если будут накладываться когерентные волны. Волны, у которых разность фаз не зависит от времени, называются когерентными (для этого волны должны быть монохроматичными (с одинаковой частотой или длиной волны ω1 = ω2, λ1 = λ2) и разность начальных фаз также не должна меняться с течением времени ∆j0 = const).

- условие временной когерентности.
 .
.
- условие пространственной когерентности.
Способы получения когерентных источников:



Вопрос 11. Интерференция волн.
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света. Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона. Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1 и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции. Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора  , записывается в виде
, записывается в виде
| E = a cos (ωt – kr), |
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
| E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ). |
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
| (*) |
где Δ = r2 – r1 – так называемая разность хода.
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2,...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
Вопрос 12. Интерференционные полосы, получающиеся на пленке переменной толщины (в отраженном или проходящем свете) при освещении ее параллельным светом, называются полосами равной толщины.

При освещении пленки переменной толщены белым светом на пленке будут наблюдаться разноцветные полосы равной толщины.
| 2′ |
| 1′ |
| R |
| O |
| 2 |
| 1 |
| rm |
| d |
Между стеклянной линзой и стеклянной пластинкой образуется тонкая пленка переменной толщины (либо воздушная с n = 1, либо заполненные какой-либо жидкостью или газом с показателем преломления n).
При нормальном падении света на линзу ( α = 0 ) оптическая разность хода отраженных (1 и 2) и проходящих (1′ и 2′) лучей будет вычисляться из формулы:
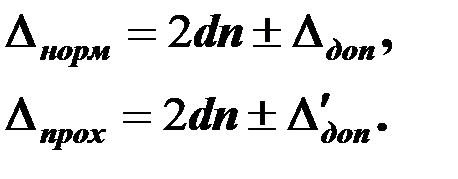 (1-13)
(1-13)
Интерференционные полосы будут наблюдаться в точках, где толщина пленки будет одинаковой, т.е. в виде концентрических колец.
Для оптически менее плотной среды пленки, чем стекло, радиусы светлых (max) и темных (min) полос (колец) в отраженном свете будут определяться по формулам:
 (1-14)
(1-14)
где R – радиус кривизны линзы.
В проходящих лучах формулы меняются местами.
При освещении установки белым светом будут наблюдаться разноцветные полосы Ньютона. 

Вопрос 13. Интерферометр Майкельсона — двухлучевой интерферометр, изобретённый Альбертом Майкельсоном. Данный прибор позволил впервые измерить длину волны света. В опыте Майкельсона интерферометр был использован Майкельсоном для проверки гипотезы о светоносном эфире. Конструктивно состоит из светоделительного зеркала, разделяющего входящий луч на два, которые в свою очередь, отражаются зеркалом обратно. На полупрозрачном зеркале разделённые лучи вновь направляются в одну сторону, чтобы, смешавшись на экране, образовать интерференционную картину. Анализируя её и изменяя длину одного плеча на известную величину, можно по изменению вида интерференционных полос измерить длину волны, либо, наоборот, если длина волны известна, можно определить неизвестное изменение длин плеч. Радиус когерентности изучаемого источника света или другого излучения определяет максимальную разность между плечами интерферометра.
Устройство используется и сегодня в астрономических, физических исследованиях, а также в измерительной технике. В частности, интерферометр Майкельсона лежит в основе оптической схемы современных лазерных гравитационных антенн.
Интерферометр Майкельсона имеет две конфигурации:
· Зеркала интерферометра установлены строго перпендикулярно друг другу;
· Зеркала интерферометра установлены не строго перпендикулярно друг другу.
Поиск по сайту:
