 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Билет11
|
Читайте также: |
Билет1
Многократное повторение испытания может привести или не привести к появлению события А. такие события принято называть случайными: к ним можно отнести появление в кабинете врача больного с данной болезнью, выпадение определенной стороны монеты при ее бросании и др.
Количественная оценка закономерностей относящихся к случайным событиям дается в разделе математики, называемой теорией вероятностей
Вероятностью случайного события назовем предел, к которому стремится частота события при неограниченном увеличении числа испытаний:
 вероятностью можно назвать отношение благоприятствующих случаев к общему числу равновозможных несовместных событий: Р(А) = m/n
вероятностью можно назвать отношение благоприятствующих случаев к общему числу равновозможных несовместных событий: Р(А) = m/n
события, которые при данных испытаниях не могут произойти, называются невозможными: их вероятность равна нулю.Событие, которое при данном испытании обязательно произойдет, называется достоверным, его вероятность равна 1.Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей. Для двух несовместных событий Р(А или В) = Р(А) + Р(В) Если два события единственно возможны и несовместны, то их называют противоположными. Сумма вероятностей двух противоположных событий, как следует из теоремы сложения вероятностей, равна единице:
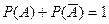 Систему событий (А1, А2,... Ak) называют полной, если при испытаниях наступит одно и только одно из этих событий. Сумма вероятностейсобытий, образующих полную систему, равна единице.Теорема умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий Р(А и В) = Р(А) • Р(В).
Систему событий (А1, А2,... Ak) называют полной, если при испытаниях наступит одно и только одно из этих событий. Сумма вероятностейсобытий, образующих полную систему, равна единице.Теорема умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий Р(А и В) = Р(А) • Р(В).
| X | Х1 | Х2 | Х3 | Х4 | Х5 | … |
| Р | p1 | p2 | рз | р4 | р5 | … |
Билет2Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.Случайная величина называется дискретной, если она принимает счетное множество значенийНепрерывная случайная величина принимает любые значения внутри некоторого интервала Распределение дискретной случайной величины.Дискретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности. Обозначим дискретную случайную величину X, ее значения хг х2,..., а вероятности Р(х1) — p1, Р(х2) = р2 и т. д. Совокупность X и Р называется распределением дискретной случайной величины (табл. 1).
Таблица 1 
Здесь предполагается, что дискретная случайная величина имеет п значений. Выражение (2.9) называется условием нормировки. Числовые характеристики случайной величины:Математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = М [ Х - М(Х) ]2 Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:
 . Распределение и характеристики непрерывной случайной величины. Непрерывную случайную величину нельзя задать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.Пусть dP — вероятность того, что непрерывная случайная величина X принимает значения между х и х + dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP ¥ dx. Кроме того, вероятность должна зависеть и от самой случайной величины, вблизи которой расположен интервал, поэтому dP = f(x)dx, (2.15) где f(x) — плотность вероятности, или функция распределения вероятностей. Она показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой этой величины: f(x) = dP/dx. (2.16) Интегрируя выражение (2.15) в соответствующих пределах, находим вероятность того, что случайная величина принимает какое-либо значение в интервале (ab):
. Распределение и характеристики непрерывной случайной величины. Непрерывную случайную величину нельзя задать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.Пусть dP — вероятность того, что непрерывная случайная величина X принимает значения между х и х + dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP ¥ dx. Кроме того, вероятность должна зависеть и от самой случайной величины, вблизи которой расположен интервал, поэтому dP = f(x)dx, (2.15) где f(x) — плотность вероятности, или функция распределения вероятностей. Она показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой этой величины: f(x) = dP/dx. (2.16) Интегрируя выражение (2.15) в соответствующих пределах, находим вероятность того, что случайная величина принимает какое-либо значение в интервале (ab):
 (2.17)
(2.17)
Условие нормировки для непрерывной случайной величины имеет вид
 (2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины:
(2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины:
 (2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:
(2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:

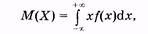 Для непрерывной случайной величины математическое ожидание и дисперсия записываются соответственно в виде
Для непрерывной случайной величины математическое ожидание и дисперсия записываются соответственно в виде
(2.20) 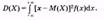 В теории вероятностей и математической статистике, в различных приложениях важную роль играет портальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность вероятности ее имеет вид
В теории вероятностей и математической статистике, в различных приложениях важную роль играет портальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность вероятности ее имеет вид
 де а = М(Х) — математическое ожидание случайной величины; а — среднее квадратическое отклонение; следовательно, s2 — дисперсия случайной величины.Кривая нормального закона распределения имеет колоколообразную форму (рис. 2.1), симметричную относительно прямой х = а (центр рассеивания). В точке х = а функция достигает максимума:
де а = М(Х) — математическое ожидание случайной величины; а — среднее квадратическое отклонение; следовательно, s2 — дисперсия случайной величины.Кривая нормального закона распределения имеет колоколообразную форму (рис. 2.1), симметричную относительно прямой х = а (центр рассеивания). В точке х = а функция достигает максимума: 
 \
\
Билет3
Математическая статистика -наука о математических методах систематизации и использования статистических данных для решения научных и практических задач. Главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют.
Большая статистическая совокупность, из которой отбирается часть объектов для исследования, называется генеральной совокупностью, а множество объектов, отобранных от неё – выборочной совокупностью, или выборкой. Выборка должна быть представительной. Так, например, если целью является изучения создоровья населения большого города, то нельзя воспользоваться выборкой населения, проживающего в одном из районов города.
Статистическое распределение, состоящее из вариант и соответствующих им частот, получило название вариационного ряда. Наряду с точечным статистическим распределением, используют интервальное статистическое распределение.
Хо, X1 X1,X2 Xi-1, Xi Xk-1, Xk
N1 n2 ni nk
Полигон частот - ломанная линия, отрезки которой соединяют точки с координатами (х1;n1), (х2;n2), …или для полигона относительных частот- с координатами (х1; p1), (x2; р2).

Гистограмма частот - совокупность смежных прямоугольников, построенных на одной прямой линии, основания прямоугольников одинаковы и равны а, а высоты равны отношению частоты к а.

Мода (Мо) равна варианте, которой соответствует наибольшая частота. В распределении массы новорожденных Мо =3,3
Медиана (Ме) равна варианте, которая расположена в середине статистического распределения. Она делит статистический ряд на две равные части. При четном числе вариант за медиану принимают среднее значение из двух центральных вариант.
Выборочная средняя (Хв) определяется как среднее арифметическое значение вариант статистического ряда:
Хв = 

Для характеристики рассеяния вариант вокруг своего среднего значения Хв вводят характеристику, называемую выборочной дисперсией, - среднее арифметическое квадратов отклонения вариант от их среднего значения:
Dв = 

Квадратный корень из выборочной дисперсии называют выборочным средним квадратичным отклонением:
Qв = 
Билет4 Предположим, что генеральная совокупность является нормальным распределением (здесь вместо вероятности следует использовать относительную частоту). Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратическим отклонением. Поэтому если по выборке можно оценить, т. е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики — определение параметров большого массива по исследованию его части.Как и для выборки, для генеральной совокупности можно определить генеральную среднюю  — среднее арифметическое значение всех величин, составляющих эту совокупность. Учитывая большой объем этой совокупности, можно полагать, что генеральная средняя равна математическому ожиданию:
— среднее арифметическое значение всех величин, составляющих эту совокупность. Учитывая большой объем этой совокупности, можно полагать, что генеральная средняя равна математическому ожиданию:  (3.10) где X — общая запись случайной величины (значения изучаемого признака) генеральной совокупности.Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией
(3.10) где X — общая запись случайной величины (значения изучаемого признака) генеральной совокупности.Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией 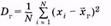 где N — объем генеральной совокупности, или генеральным средним квадратическим отклонением
где N — объем генеральной совокупности, или генеральным средним квадратическим отклонением

· Точечная оценка. Предположим, что из генеральной совокупности производятся разные выборки; делают это так, чтобы вся генеральная совокупность сохранялась неизменной. Для определенности будем считать объемы этих выборок одинаковыми и равными п. Их выборочные средние  являются случайными величинами, которые распределены по нормальному закону (см. конец § 2.3), а их математическое ожидание равно математическому ожиданию генеральной совокупности, т. е. генеоалъной средней:
являются случайными величинами, которые распределены по нормальному закону (см. конец § 2.3), а их математическое ожидание равно математическому ожиданию генеральной совокупности, т. е. генеоалъной средней:
 (3.13) На практике иногда при достаточно большой выборке за генеральную среднюю приближенно принимают выборочную среднюю.Для дисперсий положение получается несколько иным. Математическое ожидание дисперсий различных выборок [M(DBi)], составленных из генеральной совокупности, отличается от генеральной дисперсии:
(3.13) На практике иногда при достаточно большой выборке за генеральную среднюю приближенно принимают выборочную среднюю.Для дисперсий положение получается несколько иным. Математическое ожидание дисперсий различных выборок [M(DBi)], составленных из генеральной совокупности, отличается от генеральной дисперсии:
 (3.14)
(3.14) 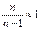 При большом п получаем иDг» M(DBi) (3.14а Для генерального среднего квадратического отклонения соответственно из (3.14) и (3.14а) получаем:
При большом п получаем иDг» M(DBi) (3.14а Для генерального среднего квадратического отклонения соответственно из (3.14) и (3.14а) получаем:

· Интервальная оценка генеральной средней при малой выборке.
При достаточно большом объеме выборки можно сделать вполне надежные заключения о генеральной средней. Однако на практике часто имеют дело с выборками небольшого объема (п < 30). В этом случае в выражении доверительного интервала (3.16) точность оценки определяется по следующей формуле:
 (3.26)
(3.26)
где t — параметр, называемый коэффициентом Стьюдента (его находят из распределения Стьюдента; оно здесь не рассматривается), который зависит не только от доверительной вероятности р, но и от объема выборки п. Коэффициент Стьюдента можно найти из табл. 8.
Запишем неравенство (3.16), подставив в него выражение 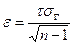 из формулы (3.26):
из формулы (3.26):
 (3.27
(3.27
Билет6
Свободными колебаниями называют такие, которые совершаются без внешних воздействий за счёт первоначально полученной телом энергии. Характерными моделями таких механических колебаний являются материальная точка на пружине и материальная точка на нерастяжимой нити. Здесь колебания возникают либо за счёт первоначальной потенциальной энергии, либо за счёт кинетической, либо за счёт и той и другой энергии.
F = -kx, k – коэффициент пропорциональности между силой и смещением, который в данном случае является жесткостью пружины; знак минус показывает, что сила всегда направлена в сторону положения равновесия.
Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.
F = F0 cos wt, где F0 – амплитуда, w – круговая частота колебаний вынуждающей силы.
Амплитуда вынужденного колебания прямо пропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от коэффициента затухания среды и круговых частот собственного и вынужденного колебаний. Если w и b для системы заданы, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление – достижение максимальной амплитуды вынужденных колебаний для заданных w и b – называют резонансом.
Гармоническое колебание: х = А cos (w0t + ф0)? Где w0t + ф0 = ф – фаза колебаний, ф0- начальная фаза, w0- круговая частота колебаний, А- их амплитуда. Амплитуда и начальная фаза колебаний определяются начальными условиями движения, т.е. положением и скоростью материальной точки в момент t =0. Среди разных видов колебаний гармоническое колебание является наиболее простой формой. Материальная точка, подвешенная на пружине совершает гармонические колебания, если не учитывать силы сопротивления.
При преобразовании дифференциального уравнения величина w0 была введена формально, но она имеет важный физический смысл, так как определяет частоту колебаний v =  системы и показывает, от каких факторов эта частота зависит: от жесткости пружины и массы, длины нити и ускорения свободного падения в другом.
системы и показывает, от каких факторов эта частота зависит: от жесткости пружины и массы, длины нити и ускорения свободного падения в другом.
Очень удобно изображать гармонические колебания с помощью векторных диаграмм. Этот метод состоит в следующем. Из начала оси абсцисс проведём вектор А, проекция которого на ось ОХ равна Acos ф. Если вектор А будет равномерно вращаться с угловой скоростью w0 против часовой стрелки, то ф = w0t+ф0. В таком представлении амплитуда колебаний есть модуль равномерно вращающегося вектора А, фаза колебаний – угол между вектором А и осью ОХ, начальная фаза- начальное значение этого угла, круговая частота колебаний- угловая скорость вращения вектора А, смещение х колеблющейся точки- проекция вектора А на ось ОХ.
Билет8
Затухающие колебания — колебания, энергия которых уменьшается с течением времени.
Уравнение затухающих колебаний

Логарифмический декремент затухания – величина, равная натуральному логарифму отношения двух последовательных амплитуд, разделенных интервалом времени, равным периоду колебаний.

Добротность - параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.добротность выражается с точностью до 2П отношение энергии в данный момент времени к убыв энергии за один период колебания
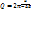
Билет9
Вынужденные колебания- это колебания,возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.
Уравнение установившихся вынужденных колебаний, совершаемых под действием внешней гармонической силы: x=Acos(ὼt+φ0)
Амплиту́дно-часто́тная характери́стика (частотная характеристика) — зависимость амплитуды синусоидального колебания на выходе устройства от частоты входного гармонического сигнала; измеряется по изменению частоты сигнала (при постоянной амплитуде колебания) на входе устройства и при линейном режиме его работы. Амплитудно-частотная характеристика показывает, как передаются его отдельные гармонические составляющие, и позволяет оценить искажения его спектра. Для наглядности амплитудно-частотную характеристику строят в виде графика: по оси ординат откладывают амплитуды или относительные амплитуды, а по оси абсцисс — частоты, иногда в логарифмическом масштабе. В электротехнике, радиоэлектронике по амплитудно-частотной характеристике определяют различные параметры (полосу пропускания частот, избирательность), по которым судят о работе устройств и приборов.
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Явление резонанса заключается в резком увеличении амплитуды установившихся вынужденных колебаний при совпадении частоты собственных колебаний системы с частотой вынуждающей силы.
Фа́зочасто́тная характеристика (ФЧХ) — зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.В теории управления ФЧХ звена определяется тангенсом отношения мнимой части передаточной функции к действительной:
 Незатухающие колебания, существующие в какой-либо системе с затуханием при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы- автоколебательными. Классическим примером механической автоколебательной системы являются часы, в которых маятник или баланс являются колебательной системой, пружина или поднятая гиря- источником энергии, а анкер- регулятором поступления энергии от источника в колебательную систему. Многие биологические системы (сердце, легкие и др.) являются автоколебательными.
Незатухающие колебания, существующие в какой-либо системе с затуханием при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы- автоколебательными. Классическим примером механической автоколебательной системы являются часы, в которых маятник или баланс являются колебательной системой, пружина или поднятая гиря- источником энергии, а анкер- регулятором поступления энергии от источника в колебательную систему. Многие биологические системы (сердце, легкие и др.) являются автоколебательными.
Билет11
Объемная плотность энергии синусоидальной волны

Волновой процесс связан с распространением энергии (Е) в пространстве. Количественной энергетической характеристикой этого процесса является поток энергии (Ф) - отношение энергии, перенесенной волной через некоторую поверхность, ко времени (t), за которое этот перенос совершается. Если перенос энергии осуществляется равномерно, то: Ф = Е / t, а для общего случая поток представляет производную от энергии по времени - Ф = d Е / d t. Единица измерения потока энергии совпадает с единицей мощности Дж/ с = Вт. Интенсивность волны (или плотность потока энергии) (I) - отношение потока энергии к площади (S) поверхности, расположенной перпендикулярно направлению распространения волны. Для равномерного распределения энергии по поверхности, через которую проходит волна I = Ф / S Измеряется интенсивность в Вт / м2.Представим в виде параллелепипеда длиной l участок среды, в которой распространяется волна. Площадь грани параллелепипеда, которая перепендикулярна направлению скорости волны v, обозначим через S (см.рис.9). Введемобъемную плотность энергии колебательного движения w, представляющую количество энергии в единице объема:
w = Е / V. За время t через площадку S пройдет энергия, равная произведению величины объема V = l S = v t S на объемную плотность энергии: Е = w v t S. (25)Разделив левую и правую части формулы (25) на время и площадь, получим выражение, связывающее интенсивность волны и скорость ее распространения. Вектор  , модуль которого равен интенсивности волны, а направление совпадает с направлением ее распространения носит название вектора Умова:
, модуль которого равен интенсивности волны, а направление совпадает с направлением ее распространения носит название вектора Умова:



Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции зависит от разности фаз накладывающихся волн.
Стоячие волны. Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны


и уравнение отраженной волны

Эффектом Доплера называют изменение частоты волн, воспринимаемых наблюдателем(приемником волн), вследствие относительного движения источника волн и наблюдателя.
Эффект Доплера находит широкое применение и в науке, и в быту. Во всем мире он используется в полицейских радарах, позволяющих отлавливать и штрафовать нарушителей правил дорожного движения, превышающих скорость. Пистолет-радар излучает радиоволновой сигнал (обычно в диапазоне УКВ или СВЧ), который отражается от металлического кузова вашей машины. Обратно на радар сигнал поступает уже с доплеровским смещением частоты, величина которого зависит от скорости машины. Сопоставляя частоты исходящего и входящего сигнала, прибор автоматически вычисляет скорость вашей машины и выводит ее на экран.
Поиск по сайту: