Орбитали существуют разной формы

s- орбиталь сферической формы, p-орбиталь имеет форму объёмной восьмерки.d и f –орбитали еще более сложной формы.

Электронный уровень (n) Сколько может разместиться электронов на данном уровне 2n²

1 2

2 8

3 18

4 32

Билет7

· Сложение гармонических колебаний, направленных по одной прямой. Пусть материальная точка одновременно участву­ет в двух колебаниях, происходящих вдоль одной линии. Анали­тически такие колебания выражаются следующими уравнениями:

Допустим, что частоты скла­дываемых колебаний одинаковы тогда результи­рующее смещение точки

Выполним такое сложение с по­мощью векторной диаграммы. Изо­бразим положение векторов и в начальный момент времени (рис. 5.9), углы между этими век­торами и осью ОХ равны начальным фазам слагаемых колебаний j₀₁ и j₀₂. Вектор — амплитуда результирующего колебания. Так как и вращаются с одинаковой угловой скоростью, то и сумма их — вектор — будет вращаться с той же угловой скоро­стью, т. е. результирующее движение является гармоническим с круговой частотой

(5.29)

Выразим амплитуду А этого колебания и начальную фазу j₁ через заданные значения Применяя теорему косинусов к треугольнику, заштрихованному на рис. 5.9, получаем

Так как –cos b = -cos [p - (j₀₂ - j₀₁)] = cos (j₀₂ - j₀₁), то

(5.30)

Как видно из рис. 5.9, tg j равен отношению проекции на ось OY к проекции на ось ОХ, т. е. А_у /А_х. Учитывая, что проек­ция суммы равна сумме проекций, имеем

(5.31)

Таким образом, поставленная задача решена: по формулам (5.30) и (5.31) можно найти амплитуду и начальную фазу резуль­тирующего колебания. Из выражения (5.30) вытекают следую­щие частные случаи: и тогда т. е. амплитуда результирующего колебания равна сумме ампли­туд слагаемых колебаний, если разность начальных фаз равна четному числу p (рис. 5.10, а);

тогда

т. е. амплитуда результирующего колебания равна разности амп­литуд слагаемых колебаний, если разность начальных фаз равна нечетному числу p (рис. 5.10, б). В частности, при A₁ = A₂ имеем А = О, т. е. колебания нет (рис. 5.10, в). Это достаточно очевидно: если материальная точка участвует одновременно в двух колеба­ниях, имеющих одинаковую амплитуду и совершающихся в противофазе, то точка неподвижна. Если частоты складываемых ко­лебаний не одинаковы, то сложное колебание уже не будет гармо­ническим.

· БИЕНИЯ - периодич. изменения во времени амплитуды колебания, возникающего при сложении двух гармонических колебаний с близкими частотами. Б. появляются вследствие того, что величина разности фаз между двумя колебаниями с разл. частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через нек-рое время в противофазе, затем снова в фазе и т. д. Соответственно амплитуда результирующего колебания периодически достигает то максимума, равного сумме амплитуд складываемых колебаний, то минимума, равного разности этих амплитуд (рис.). Напр., Б. возникают при звучании двух камертонов с близкими частотами - звук поочерёдно усиливается и ослабевает, при сложении нормальных колебаний с близкими частотами в связанных линейных осцилляторах.

Биения, возникающие в результате сложения двух гармонических колебаний с одинаковыми амплитудами и близкими частотами.

При сложении двух бегущих в одном направлении волн с близкими частотами и волновыми числами Б. возникают не только во времени, но и в пространстве. Складывая, напр., волны с равными амплитудами

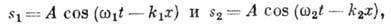
получаем результирующую волну

с частотой и волновым числом 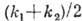, к-рые близки к частоте и волновому числу любой из компонент. Амплитуда волны модулирована в пространстве и времени медленно меняющейся огибающей с частотой 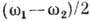и волновым числом . Частота Б. равна разности частот складываемых компонент .

При сложении двух волн с равными частотами и разными, но близкими по направлению волновыми векторами Б. возникают только в пространстве в результате интерференции волн (т. н. муар). Именно такую структуру имеют волны в френелевской зоне излучателей, а также волны в разл. волноводных системах.

Колебания в виде суперпозиции колебаний (или волн) с близкими частотами могут возникать в нелинейных системах. Так, если на нелинейное устройство, напр. квадратичный детектор, подать сумму двух колебаний, получим:

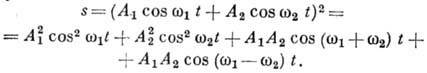
Последнее слагаемое - колебание с разностной частотой - наз. разностным тоном или тоном Б. Режимом Б. наз. также режим модуляции результирующего колебания разностной частоты, возникающий при действии на нелинейный осциллятор внеш. колебания с близкой частотой.

Измерение тона Б. лежит в основе точных измерений малых разностей двух близких частот, в частности сравнения нек-рой измеряемой частоты с эталонной.

· Ж.. Фурье показал, что периодическая функция любой сложнос­ти может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции.

Такое разложение периодической функции на гармонические составляющие и, следовательно, разложение различных периоди­ческих процессов (механические, электрические и т. п.) на гармо­нические колебания называется гармоническим анализом. Су­ществуют математические выражения, которые позволяют найти составляющие гармонические функции. Автоматически гармони­ческий анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами — анализаторами.

Совокупность гармонических колебаний, на которые разложе­но сложное колебание, называется гармоническим спектром сложного колебания.

Гармонический спектр удобно представить как набор частот (или круговых частот) отдельных гармоник совместно с соответст­вующими им амплитудами. Наиболее наглядно такое представле­ние выполняется графически. В качестве примера на рис. 5.16, а изображены графики сложного колебания (кривая 4) и составляю­щих его гармонических колебаний (кривые /, 2 и 3); на рис. 5.16, б показан гармонический спектр, соответствующий этому примеру.

Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс, он находит применение в акустике, радиотехнике, электронике и других областях науки и техники.

· Сложение взаимно перпендикулярных гармонических колебаний. Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое — вдоль оси OY. Колебания заданы следующими уравнениями:

(5.34)

Допустим, что частоты колебаний одинаковы, т. е. тогда

(5.35)

Уравнения (5.35) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные значения t, то можно определить координаты х и у, а сово­купность координат и есть траектория. Более наглядно траекторию можно представить в виде зависимости у = f(x), для получения ко­торой следует исключить время из уравнений (5.35). Произведя ма­тематические преобразования, получим уравнение эллипса:

(5.36)

Таким образом, при одновременном участии в двух взаим­но перпендикулярных гармонических колебаниях одинаковой частоты материальная точка движется по эллиптической траектории (рис. 5.12).

Из выражения (5.36)вытекают некоторые частные случаи:

Это каноническая форма уравнения эллипса, соответствующая симметричному расположению его относительно осей координат (рис. 5.13, а). Из (5.37) при А₁ = А₂ = R (рис. 5.13, б) получаем уравнение окружности радиусом R:

(5.38)

тогда

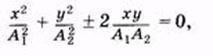(5.39)

и после преобразований

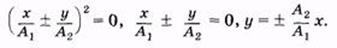(5.40)

Поиск по сайту: