Билет18

Гидродинамика — это раздел гидравлики, изучающий законы механического движения жидкости и ее взаимодействия с неподвижными и подвижными поверхностями. Основная задача гидродинамики: определение гидродинамических характеристик потока, таких как гидродинамическое давление, скорость движения жидкости, сопротивление движению жидкости, а также изучение их взаимосвязи.

Стационарное течение жидкости - это такое течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению. Для стационарного течения форма и расположение линий тока со временем не изменяются.

Условие неразрывности струи: при стационарном течении несжимаемой жидкости через любые сечения трубки тока каждую секунду протекают одинаковые объемы жидкости, равные произведению площади сечения на среднюю скорость движения ее частиц.

Уравнение (7.1) выражает условие неразрывности струи. Оно устанавливает соотношение между скоростями течения жидкости в различных сечениях трубки тока:

Рассмотрим стационарное течение идеальной жидкости. Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. Рассмотрим объём жидкости V, ограниченный стенками трубки токаи и перпендикулярными к линиям тока сечениями S1 и S2. За время Δt этот объём переместится. В силу непрерывности струи:

ΔV1 = ΔV2 = ΔV

Энергия каждой частицы жидкости складывается из её кинетической и потенциальной энергии. Вследствие стационарности течения приращение энергии ΔЕ всего рассматриваемого объёма V можно вычислить как разность энергий заштрихованных объёмов ΔV1 и ΔV2.

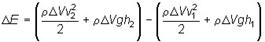
где ρ — плотность жидкости.

В идеальной жидкости приращение энергии должно равняться работе, совершаемой над выделенным объёмом силами давления:

ΔЕ = А (1)

А = P1S1Δl1 — P2S2Δl2 = (P1 — P2)ΔV.

Подставляя в (1) и сократив ΔV, получим:

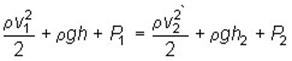
Поскольку сечения S1 и S2 произвольные, то это справедливо в любом сечении трубки тока. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие:

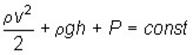– уравнение Бернулли.

Для горизонтальной линии тока уравнение Бернулли примет вид:

,

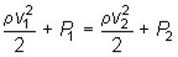т.е. давление оказывается меньшим в тех точках, где скорость больше.

При движении реальной жидкости между ее слоями возникают силы внутреннего трения, или силы вязкости. Со стороны слоя, движущегося более быстро, за счет сил межмолекулярного сцепления действует ускоряющая сила, а со стороны слоя, движущегося более медленно, на более быстрый слой действует замедляющая сила. Эти силы направлены по касательной к поверхности слоев и называются силами внутреннего трения. В газах возникновение сил внутреннего трения обусловлено в основном переходом молекул между движущимися слоями. Пусть два слоя жидкости, которые находятся на расстоянии ∆z друг от друга, движутся со скоростями 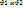Обозначим 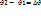Отношение 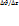характеризует, как быстро изменяется скорость от слоя к слою в направлении, перпендикулярном скорости движения слоев, и называется градиентом скорости. Как показал Ньютон, сила внутреннего трения пропорциональна градиенту скорости и площади соприкасающихся слоев текущей жидкости

F= η S где η — коэффициент динамической вязкости.

Течение жидкости называется ламинарным (слоистым), если выделенный вдоль потока слой скользит относительно соседних, не перемешиваясь с ними. Ламинарное течение стационарно. Течение жидкости называется турбулентным (вихревым), если в потоке происходит перемешивание частиц жидкости. Турбулентное течение нестационарно.

Английский физик Осборн Рейнольдс (1842—1912), исследуя характер течения жидкостей по трубам, установил, что переход от ламинарного течения к турбулентному определяется безразмерным числом, которое получило название числа Рейнольдса:

Re =

где ρ — плотность жидкости, υ — средняя скорость потока по сечению трубы, η

— коэффициент динамической вязкости, l — характерный размер сечения потока

(пр Соотношение (8.12) было установлено французским физиком и физиологом

Жаном Пуазейлем (1799—1869) и получило название формулы Пуазейля. и течении в длинных цилиндрических трубах l равно диаметру).

V = (p2-p1)t

Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода - это линейные потери; в других - они сосредоточены на очень коротких участках, длиной которых можно пренебречь, - на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.

Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

Поиск по сайту: