 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Векторы и операции над ними
Вектором называется направленный отрезок, который можно перемещать параллельно самому себе. Векторы могут обозначается несколькими способами. Например, 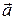 либо a, или
либо a, или 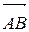 , где точка
, где точка  означает начало вектора, а точка
означает начало вектора, а точка  – конец вектора.
– конец вектора.
Длиной вектора 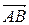 называется число, равное длине отрезка
называется число, равное длине отрезка 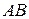 , изображающего вектор. Длина вектора обозначается
, изображающего вектор. Длина вектора обозначается  .
.
 Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Вектор, длина которого равна нулю, называется нуль-вектором. Нуль-вектор обозначается 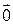 .
.
Произведением вектора 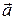 на число
на число  называется вектор
называется вектор  , имеющий длину
, имеющий длину 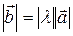 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 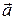 , если
, если  , и противоположно ему, если
, и противоположно ему, если  .
.
Пусть 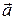 и
и  – два произвольных вектора. Возьмем произвольную точку
– два произвольных вектора. Возьмем произвольную точку  и построим вектор
и построим вектор 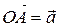 . От точки
. От точки  отложим вектор
отложим вектор 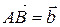 . Вектор
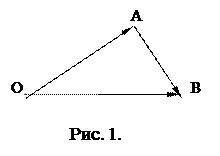
. Вектор 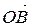 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов 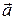 и
и  :
:  . (см. рис. 1) Это правило сложения векторов называется правилом треугольника.
. (см. рис. 1) Это правило сложения векторов называется правилом треугольника.
 Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку
Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку  и откладывают от нее два вектора
и откладывают от нее два вектора 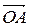 и
и  . Далее на этих векторах достраивают параллелограмм
. Далее на этих векторах достраивают параллелограмм 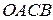 . Диагональ
. Диагональ 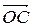 является суммой векторов
является суммой векторов 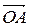 и
и  .
.
Разностью двух векторов 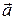 и
и  называется вектор
называется вектор 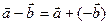 . (см. рис. 2)
. (см. рис. 2)
Введем понятие координат вектора. Для этого совместим начало вектора 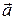 с началом координат. Тогда координатами вектора
с началом координат. Тогда координатами вектора 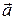 называются координаты его конечной точки.
называются координаты его конечной точки.
Пусть точка  имеет координаты
имеет координаты  , а точка
, а точка  –
–  . Тогда координаты вектора
. Тогда координаты вектора 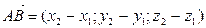 .
.
Суммой векторов  и
и 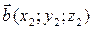 является вектор
является вектор  .
.
Разностью векторов  и
и 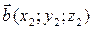 является вектор
является вектор 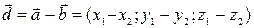 .
.
Произведением вектора  на число
на число  называется вектор
называется вектор 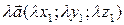 .
.
Длина вектора 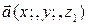 равна
равна 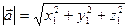 .
.
Скалярным произведением векторов 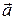 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 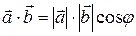 , где
, где 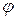 – угол между векторами
– угол между векторами 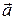 и
и  .
.
Если вектора 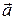 и
и  заданы с помощью координат, то скалярное произведение векторов равно:
заданы с помощью координат, то скалярное произведение векторов равно:  .
.
Заметим, что скалярный квадрат вектора равен квадрату его длины:  .
.
Угол между векторами 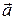 и
и  вычисляется по формуле:
вычисляется по формуле:
 .
.
Пример. Даны два вектора  и
и 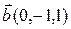 . Найти угол между этими векторами.
. Найти угол между этими векторами.
Решение. Вычислим косинус угла между этими векторами:
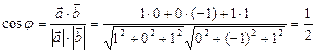 . Следовательно,
. Следовательно,  .
.
Ответ:  .
.
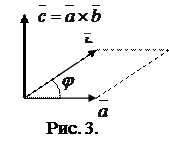 Векторное произведение
Векторное произведение 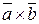 (другое обозначение
(другое обозначение 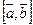 ) двух векторов
) двух векторов  и
и  есть третий вектор
есть третий вектор  , модуль которого
, модуль которого  (т. е. равен площади параллелограмма, построенного на векторах
(т. е. равен площади параллелограмма, построенного на векторах  и
и  ), а направление перпендикулярно к обоим векторам
), а направление перпендикулярно к обоим векторам  и
и  (т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от
(т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от  к
к  на угол, меньший
на угол, меньший 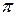 (рис 4.) Из этого определения векторного произведения следует, что векторы
(рис 4.) Из этого определения векторного произведения следует, что векторы  ,
,  и
и 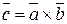 образуют правую систему.
образуют правую систему.
Если векторы  и
и  коллинеарны (
коллинеарны (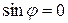 ), то
), то 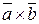 =0.
=0.
Свойства векторного произведения:
1) 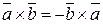 ;
;
2)  ;
;
3) 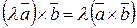 ;
;
4)  ;
;
5) 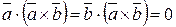 .
.
Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям:
 ;
;  ;
; 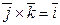 ;
; 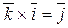 .
.
Если векторы  и
и  заданы своими декартовыми координатами:
заданы своими декартовыми координатами:  ,
,  , то их векторное произведение
, то их векторное произведение
 .
.
Смешанным произведением векторовназывается произведение 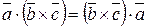 , результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение
, результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение  . Если векторы
. Если векторы  ,
,  и
и  образуют правую тройку, то
образуют правую тройку, то 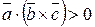 , если – левую, то
, если – левую, то 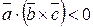 .
.
 Смешанное произведение
Смешанное произведение 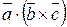 равно объему параллелепипеда
равно объему параллелепипеда  , построенного на векторах
, построенного на векторах  ,
,  и
и  , взятому со знаком «+», если векторы
, взятому со знаком «+», если векторы  ,
,  и
и  образуют правую тройку, и со знаком «–», если – левую:
образуют правую тройку, и со знаком «–», если – левую:
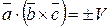 .
.
Если векторы  ,
,  и
и  заданы своими декартовыми координатами:
заданы своими декартовыми координатами:  ,
,  ,
, 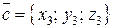 , то их смешанное произведение
, то их смешанное произведение
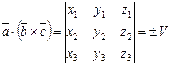 .
.
Пример. Даны координаты вершин треугольника:  ,
,  ,
, 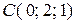 . Найти площадь
. Найти площадь  .
.
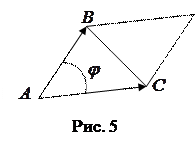 Решение. Направим из вершины
Решение. Направим из вершины  треугольника векторы в вершины
треугольника векторы в вершины  и
и 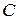 (рис. 5.). Учитывая, что площадь
(рис. 5.). Учитывая, что площадь 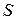
 равна половине площади параллелограмма, построенного на этих векторах, площадь которого, в свою очередь, можно выразить через векторное произведение, будем иметь
равна половине площади параллелограмма, построенного на этих векторах, площадь которого, в свою очередь, можно выразить через векторное произведение, будем иметь 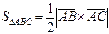 . Находим координаты векторов:
. Находим координаты векторов:  ,
,  . Находим векторное произведение
. Находим векторное произведение 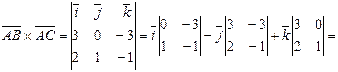
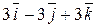 =
= 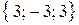 .
.
Таким образом,  (кв. ед.).
(кв. ед.).
Пример. Найти объем параллелепипеда, построенного на векторах 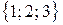 ,
, 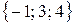 ,
,  .
.
Решение. Вычисляем смешанное произведение данных векторов:  =
=
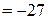 . Объем параллелепипеда
. Объем параллелепипеда  .
.
Поиск по сайту: