 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение прямой на плоскости. Существует несколько различных способов задания прямой на плоскости
Существует несколько различных способов задания прямой на плоскости.
1) уравнение прямой с угловым коэффициентом имеет вид:
 ,
,
где  – угловой коэффициент прямой,
– угловой коэффициент прямой,
 – угол, образуемый прямой с осью
– угол, образуемый прямой с осью  . (см. рис. 6)
. (см. рис. 6)
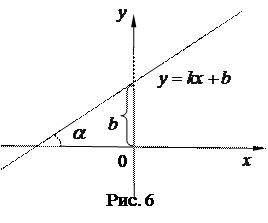
Пусть прямая проходит через точку  и образует с осью
и образует с осью  угол
угол  , тогда уравнение прямой можно представить в виде:
, тогда уравнение прямой можно представить в виде:
 . (4)
. (4)
Пример. Составить уравнение прямой проходящей через точку  и образующей с осью
и образующей с осью  угол 135°.
угол 135°.
Решение. Определим угловой коэффициент прямой 
 .
.
Подставим данные значения в формулу (4):  .
.
Упростив, получим искомое уравнение:  .
.
Ответ:  .
.
2) уравнение прямой, проходящей через две различные точки  и
и  имеет вид:
имеет вид:
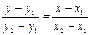 . (5)
. (5)
Пример. Составить уравнение прямой, проходящей через точки  и
и  .
.
Решение. Подставим координаты точек в формулу (5):
 .
.
Упростив, получим искомое уравнение:
 .
.
Ответ:  .
.
3) уравнение прямой в отрезках имеет вид
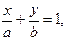 (6)
(6)
 где
где  и
и  – отрезки, отсекаемые прямой на координатных осях. (см. рис. 7)
– отрезки, отсекаемые прямой на координатных осях. (см. рис. 7)
Пример. Составить уравнение прямой, если известно, что она отсекает по оси  отрезок равный 3, а по оси
отрезок равный 3, а по оси  отрезок равный 5.
отрезок равный 5.
Решение. По условию задачи  .
.
Подставив значения  и
и  в формулу (3) получим искомое уравнение:
в формулу (3) получим искомое уравнение:
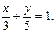
Ответ: 
4) общее уравнение прямой имеет вид
 , (7)
, (7)
где  и
и  не равны нулю одновременно.
не равны нулю одновременно.
Нормальным вектором прямой называется любой ненулевой вектор, перпендикулярный ей.
Если прямая задана в виде (7), то нормальный вектор этой прямой имеет координаты 
Всякий ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.
Если прямая задана в виде (7), то координаты направляющего вектора будут 
Пример. Составить уравнение прямой, проходящей через точку 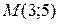 перпендикулярно вектору
перпендикулярно вектору 
Решение. Поскольку вектор  является нормальным вектором прямой, то
является нормальным вектором прямой, то  ,
,  . Подставим эти значения в уравнение (7):
. Подставим эти значения в уравнение (7):

Теперь надо определить значение 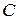 . Так как точка
. Так как точка 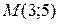 принадлежит данной прямой, то ее координаты должны удовлетворять уравнению прямой:
принадлежит данной прямой, то ее координаты должны удовлетворять уравнению прямой:

Отсюда 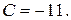
Подставив значение коэффициента 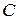 , получим искомое уравнение:
, получим искомое уравнение:

Ответ: 
Пример. Составить уравнение прямой, проходящей через точку  параллельно вектору
параллельно вектору 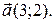
Решение. Поскольку вектор  является направляющим вектором прямой, то
является направляющим вектором прямой, то 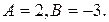 Подставим эти значения в уравнение (7):
Подставим эти значения в уравнение (7): 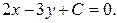
Определим значение коэффициента 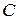 . Так как, точка
. Так как, точка  принадлежит данной прямой, то ее координаты должны удовлетворять уравнению прямой:
принадлежит данной прямой, то ее координаты должны удовлетворять уравнению прямой: 
Отсюда  Подставив значение коэффициента
Подставив значение коэффициента 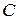 , получим искомое уравнение:
, получим искомое уравнение:

Ответ: 
Поиск по сайту: