АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Образец решения

Читайте также:
  1. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  2. MathCad: способы решения системы уравнений.
  3. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
  5. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
  8. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
  9. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ, ПО УСЛОВИЮ КОТОРЫХ ПРОИСХОДИТ ВСТРЕЧА ТЕЛ
  10. Алгоритм решения ЗЛП графическим методом
  11. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  12. Алгоритмизация процесса разработки и принятия управленческого решения

3. Вычислить , если , , .

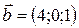Решение. , ,

.

Ответ: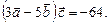

4. Даны вектора , , . Вычислить векторное произведение .

Решение. Сначала определим координаты векторов и :
.
.

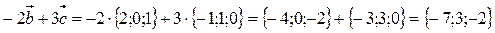Тогда векторное произведение полученных векторов:

Ответ.

5. Для треугольника с вершинами , , 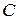найти:

а) уравнение стороны ;

б) длину высоты ;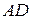

в) уравнение высоты .

Решение. а) Уравнение стороны найдем по формуле уравнения прямой, проходящей через две точки:

.

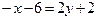
б) Высота 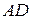– это перпендикуляр к стороне .

Тогда длина высоты ­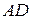 это расстояние от точки до прямой : , которое можно вычислить по формуле:

.

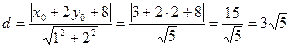в) Высота – это прямая, перпендикулярная прямой 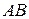, проходящая через точку 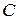. Для этого найдем уравнение прямой 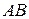по формуле:

,

,

,

,

,

,

.

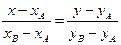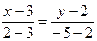Угловой коэффициент прямой 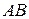равен , поэтому угловой коэффициент перпендикуляра будет равен .

Уравнение перпендикуляра найдем по формуле: ,

,

,

,

,

.

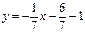Ответ: а) : 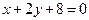, б) ; в) .


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)