Логика высказываний. Отношения атрибутивных высказываний по истинности. Логический квадрат

Среди высказываний отрицания различают высказывания с внешним и внутренним отрицанием. В зависимости от задач исследования высказывание отрицания можно рассматривать или как простое, или как сложное высказывание.

При рассмотрении высказывания отрицания как простого высказывания важной задачей является определение правильной логической формы высказывания:

- простое высказывание, содержащее внутреннее отрицание, принято относить к отрицательным высказываниям (см. «Виды атрибутивных высказывания по качеству»). Например: «Некоторые жители Республики Беларусь не пользуются банковскими кредитами», «Ни один заяц не является хищником»;

- правильной логической формой простого высказывания с внешним отрицанием является противоречащее данному высказывание с(м. «Логические отношения между высказываниями. Логический квадрат»).

Например: высказыванию «Не все люди жадные» соответствует высказывание «Некоторые люди не являются жадными».

Рассматривая высказывание отрицания как сложное высказывание, необходимо определить его логическое значение.

Исходное высказывание: Солнце светит (р).

Высказывание отрицания: Солнце не светит (┐р).

Высказывание двойного отрицания: Неверно, что солнце не светит

(┐┐р).

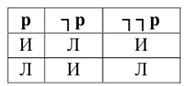
Высказывание отрицание истинно лишь тогда, когда исходное высказывание ложно, и наоборот. С высказыванием отрицания связан закон двойного отрицания: двойное отрицание произвольного высказывания равносильно самому этому высказыванию. Условия истинности высказывания отрицания изображены на рисунке

Поиск по сайту: