Изобарный

Молярная теплоёмкость при постоянном давлении обозначается как 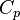. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера .

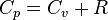Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной:

Вопрос

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОЕМКОСТИ ГАЗОВ

Микрочастицы (молекулы, атомы), из которых состоит газ, могут совершать, в общем случае, три типа движений: поступательное, вращательное, колебательное.

Атом как материальная точка может совершать только поступательное движение в трех направлениях (три степени свободы - i=3).

Молекула, состоящая из двух атомов, как система, состоящая из двух материальных точек, может совершать поступательное движение в трех направлениях (три с.с.), вращательное движение вокруг двух осей (две с.с.) и, при определенных условиях, колебательные движение вдоль оси, соединяющей атомы (одна или более с.с.). Общее число с.с. (без учета колебательных) i=5.

Молекула, состоящая из трех атомов, как система, состоящая из трех материальных точек, может совершать поступательное движение в трех направлениях (три с.с.), вращательное движение вокруг трех осей (три с.с.) и, при определенных условиях, различные колебательные движение вдоль осей соединяющей атомы (одна или более с.с.). Общее число с.с. (без учета колебательных) i=6.

Как показано в молекулярно-кинетической теории на каждую поступательную или вращательную степень свободы каждой микрочастицы приходится энергия равная (1/2)kT (закон равномерного распределения энергии по степеням свободы). Таким образом, для одного моля газа (число микрочастиц равно числу Авогадро N), внутренняя энергия газа:

U=i(1/2)kTN_А=(i/2)RT

Тогда теплоемкость газа при постоянном объеме:

C_v=(dU/dT)=(i/2)R

Без учета колебательных степеней свободы:

Для газа, состоящего из одноатомных молекул, С_v=(3/2)R

Для газа, состоящего из двухатомных молекул, С_v=(5/2)R

Для газа, состоящего из трехатомных молекул, С_v=(6/2)R

Основное уравнение МКТ. Исходя из определения среднего значения квадрата скорости и выражения (14.14), следует, что давление газа на стенку сосуда равно:

P = n·m·<v²>/3 = 2·n·<E_пост>/3, (14.15)
где <E_пост> - среднее значение энергии поступательного движения молекул.

Выражение (14.15) называется уравнением Клаузиуса или основным уравнением молекулярно-кинетической теории газов.

Давление, оказываемое молекулами идеального газа на стенки сосуда, пропорционально массе молекулы, концентрации и среднему значению квадрата скорости молекул.

Квантование — процедура построения чего-либо с помощью дискретного набора величин, например, целых чисел, в отличие от построения с помощью непрерывного набора величин, например, действительных чисел.

Вопрос

Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)^3/2 V² exp(MV²/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, градусы Кельвина, К;
М - молярная масса, кг/моль, численно равная молекулярной массе;
R = 8,3144 Дж/(моль•К) - универсальная газовая постоянная в системе СИ.

Вопрос

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

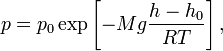
где p — давление газа в слое, расположенном на высоте h, p ₀ — давление на нулевом уровне (h = h ₀), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

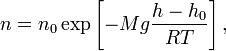
где M — молярная масса газа, R — газовая постоянная.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина 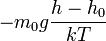, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной kT. Чем выше температура T, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m.

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле (2.4.1) на n и n₀ и получим распределение Больцмана для молярной массы газа:

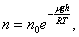
(2.5.1)

где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как 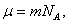а 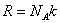, то (2.5.1) можно представить в виде

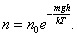
(2.5.2)

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:

,

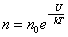(2.5.3)

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

На рисунке 2.11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

Рис. 2.11

Из (2.5.3) можно получить, что отношение концентраций молекул в точках с U₁ и i>U₂ равно:

.

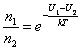(2.5.4)

Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.

Вопрос

Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега 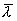- это среднее расстояние, которое проходит молекула от столкновения до столкновения.

Для определения 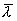вычислим сначала среднее число соударений 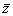выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения .

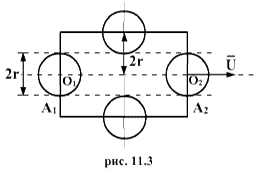
Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения 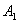в положение 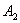по прямой (рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории . Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной , т.е.

.

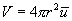Если концентрация молекул n, то внутри рассмотренного цилиндра находится число молекул, равное

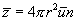
Это число 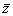и определяет среднее число соударений за единицу времени.

Предположение о том, что все молекулы, кроме одной, неподвижны, является, конечно не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости должны входить средняя относительная скорость молекул 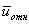. Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в 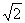раз превышает . Таким образом, среднее число соударений должно быть увеличено в 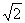раз

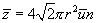
(11.7)

Средний путь, проходимый молекулой за единицу времени, численно равен . Поэтому средняя длина свободного пробега равна 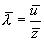или

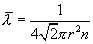
(11.8)

Таким образом, средняя длина свободного пробега 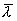не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают 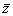и , и . При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе. Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром . Тогда

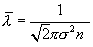
(11.9)

Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Вопрос

Круговой процесс (цикл) в термодинамике, процесс, при котором физическая система (например, пар), претерпев ряд изменений, возвращается в исходное состояние. Термодинамические параметры и характеристические функции состояния системы (температура Т, давление р, объём V, внутренняя энергия U, энтропия S и др.) в конце К. п. вновь принимают первоначальное значение и, следовательно, их изменения при К. п. равны нулю ( U = 0 и т. д.). Все изменения, возникающие в результате К. п., происходят только в среде, окружающей систему. Система (рабочее тело) на одних участках К. п. производит положительную работу за счёт своей внутренней энергии и количеств теплоты Q_n, полученных от внешних источников, а на др. участках К. п. работу над системой совершают внешние силы (часть её идёт на восстановление внутренней энергии системы). Согласно первому началу термодинамики (закону сохранения энергии), произведённая в К. п. системой или над системой работа (А) равна алгебраической сумме количеств теплоты (Q), полученных или отданных на каждом участке К. п. ( U = Q — А = 0, А = Q). Отношение А / Q_n (совершённой системой работы к количеству полученной ею теплоты) называется коэффициентом полезного действия (кпд) К. п.

Различают равновесные (точнее, квазиравновесные) К. п., в которых последовательно проходимые системой состояния близки к равновесным, и неравновесные К. п., у которых хотя бы один из участков является неравновесным процессом. У равновесных К. п. кпд максимален. На рисунке дано графическое изображение равновесного (обратимого) Карно цикла, имеющего максимальное кпд.

К. п. называется прямым, если его результатом является совершение работы над внешними телами и переход определённого количества теплоты от более нагретого тела (нагревателя) к менее нагретому (холодильнику). К. п., результатом которого является перевод определённого количества теплоты от холодильника к нагревателю за счёт работы внешних сил, называется обратным К. п. или холодильным циклом.

Тепловой двигатель — тепловая машина, превращающая тепло в механическую энергию. Использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и холодильником. Был предложен вариант вечного двигателя, нарушающего 2 закон термодинамики. Если не использовать холодильник и нагреватель, а просто встроить в поршень демона Максвелла, который будет пропускать в одну сторону горячие молекулы, а в другую холодные, то поршень придёт в движение. Если дать команду демону пропускать молекулы в другом направлении, поршень спустя какое-то время двинется в обратном направлении.

Работа, совершаемая двигателем, равна:

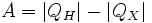,где:

Q_H — количество теплоты, полученное от нагревателя,

Q_X — количество теплоты, отданное охладителю.

Коэффициент полезного действия (КПД) теплового двигателя рассчитывается как отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя: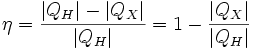

Часть теплоты при передаче неизбежно теряется, поэтому КПД двигателя менее 1. Максимально возможным КПД обладает двигатель Карно. КПД двигателя Карно зависит только от абсолютных температур нагревателя(T_H) и холодильника(T_X):

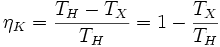
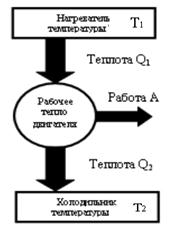Тепловые машины могут иметь разную конструкцию. Это может быть паровой двигатель, двигатель внутреннего сгорания, реактивный двигатель. Любой тепловой двигатель работает по замкнутому циклу и имеет нагреватель, рабочее тело двигателя и холодильник. В процессе работы теплового двигателя рабочее тело двигателя получает от нагревателя количество теплоты Q₁, совершает работу A и передает холодильнику количество теплоты Q₂<Q₁. Для замкнутого цикла изменение внутренней энергии равно нулю (∆U=0). Следовательно, согласно I началу термодинамики, работа, совершаемая двигателем, равна A=Q₁-Q₂ Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя η=Q₁-Q₂/Q₁ КПД тепловой машины всегда меньше единицы η=1-Q₂/Q₁ Следовательно, невозможно всю теплоту превратить в работу. Ученые всегда стремились повысить КПД. В первой половине XIX в. французский ученый Сади Карно показал, что максимально возможное значение КПД тепловой машины равно η_max=T₁-T₂/T₁=1-T₂/T₁, где T ₁ - температура нагревателя, T ₂ - температура холодильника. Из сравнения уравнений (4.18) и (4.19) следует, что η_max ≥ η или 1-T₂/T₁≥1Q₂/Q₁. Отсюда Q₂/T₂≥Q₁/T₁ На основании этого неравенства можно прийти к понятию энтропия и второму началу термодинамики. Повышение КПД тепловых двигателей и приближение его к максимально возможному значению - важнейшая техническая задача. Однако, все тепловые двигатели выделяют большое количество теплоты, что называется тепловым загрязнением, и выбрасывают в атмосферу вредные для растений и животных химические соединения.

Вопрос

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая невозможность перехода всей внутренней энергии системы в полезную работу.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины забрав тепло Q ₁ у нагревателя, отдав Q ₂ холодильнику и совершив при этом работу A = Q ₁ − Q ₂. После этого воспользуемся процессом Клаузиуса и вернем тепло Q ₂ от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны.

Теорема Карно-Клаузиуса: коэффициент полезного действия тепловой машины, работающей обратимо по циклу Карно, не зависит от природы рабочего тела машины, а лишь от температуры нагревателя и температуры холодильника.

Вопрос

Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.

Второе начало термодинамики, как и первое, имеет несколько формулировок.

Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.

Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.

К определению энтропии S можно прийти на основе анализа работы тепловых машин. Если система получает тепло (Q>0) или отдает тепло (Q<0), то состояние ее меняется. Тогда, при изменении состояния системы, можно найти не саму энтропию, а только ее изменение, т. е. ∆S=∆Q/T

Для тепловой машины изменение энтропии нагревателя и холодильника равны: ∆S₁=Q₁/T₁ и ∆S₂=Q₂/T₂

Формула ∆S=∆Q/T справедлива для изотермического процесса и представляет собой термодинамическое определение энтропии. Энтропией называется термодинамическая величина, изменение которой в системе пропорционально ее тепловой энергии, деленной на абсолютную температуру. Для любого процесса можно найти бесконечно малое изменение энтропии, т. е. ее дифференциал dS=δQ/T, где δQ- элементарная теплота

В интегральной форме для любого процесса изменение энтропии равно

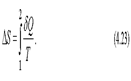Найдем изменение энтропии за один цикл для тепловой машины. Из неравенства следует, что ∆S₂≥∆S₁. Полное изменение энтропии за цикл больше или равно нулю ∆S=∆S₂-∆S₁≥0 Знак равенства ΔS = 0 относится к обратимым процессам, которые являются бесконечно медленными процессами.

Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры.

Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии. Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает. Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) - равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием (или диссипацией) энергии. Второе начало термодинамики определяет направленность тепловых процессов в изолированных системах, они всегда протекают в сторону роста энтропии, в сторону увеличения беспорядка. Возникновение упорядоченных структур возможно только в незамкнутых, т. е. в открытых системах. Открытой системой называется система, которая обменивается энергией и веществом с окружающей средой. В открытых системах энтропия может как возрастать, так и убывать в зависимости от знака Q/T.

В открытых системах, находящихся в неравновесном состоянии, при определенных условиях из хаоса может возникать порядок. Процесс возникновения из хаоса упорядоченных структур называется самоорганизацией. Процессы самоорганизации являются общими для живой и неживой природы.

Вопрос

ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ (неравновесная термодинамика), изучает общие закономерности поведения систем, не находящихся в состоянии термодинамического равновесия. В таких системах имеют место разнообразные неравновесные процессы (теплопередача, диффузия, электрич. ток, хим. р-ции и т. п.), к-рые являются необратимыми в термодинамич. смысле (см. Обратимые и необратимые процессы). Согласно ур-нию Клаузиуса, для неадиабатич. процессов изменение энтропии системы dS равно:

где d_eS = Q / T- "внешнее" изменение энтропии, связанное с обратимым теплообменом с окружающей средой (Q -бесконечно малое кол-во теплоты, T -абс. т-ра), d_iS- "внутреннее" изменение энтропии, обусловленное самопроизвольным протеканием в системе необратимых процессов. При этом d_i S 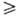О, где знак равенства относится к состоянию равновесия или к случаю обратимых (квазистатич.) процессов. Величина d_iS играет центр. роль в Т. н. п.

К осн. задачам Т. н. п. относят исследование балансов физ. величин (энергии, массы, энтропии и др.) при переходах, превращениях и диссипации энергии, а также установление законов эволюции макроскопич. систем. В этой связи в Т.н.п. появляется и играет важную роль время t- переменная, отсутствующая в равновесной термодинамике (равновесные в термодинамич. смысле процессы протекают бесконечно медленно). Поэтому вместо (1) рассматривается соотношение:

dS/dt = d_eS/dt + d_iS/dt,

где величина P = d_iS/dt наз. глобальным произ-вом энтропии (т.е. относящееся ко всему объему системы).

Различают феноменологическую Т. н. п. и статистич. теорию неравновесных процессов. Феноменологическая Т. н. п., в свою очередь, подразделяется на линейную и нелинейную теории. Обычно в Т. н. п. рассматриваются три типа систем: однородные, прерывные и непрерывные. В однородных системах в любой момент времени интенсивные св-ва (параметры состояния) - т-ра, давление, хим. потенциал - одинаковы по всему объему. Прерывные (вентильные, гетерогенные) системы состоят из двух и более однородных частей, разделенных либо границей раздела фаз, либо вентилем (напр., газы в сосудах, соединенных мембраной или капилляром), так что св-ва меняются скачком при переходе из одной части в другую. Непрерывными наз. системы, интенсивные св-ва к-рых можно считать непрерывными ф-циями координат точки внутри системы (полевых переменных) и времени.

Соотношения, характеризующие процессы переноса массы, энергии, заряда, энтропии и т.д., записываются в виде балансовых ур-ний. Такие ур-ния м. б. записаны как для непрерывных, так и для прерывных систем. В них всегда фигурируют величины двух типов, одни из к-рых трактуются как потоки, другие-как силы. Потоки характеризуют скорость переноса физ. величины (энергии, массы, энтропии и т.д.) через воображаемую единичную площадку или скорость хим. р-ции. Термодинамич. силы-это причины, порождающие потоки. Для процессов переноса в непрерывных системах силы имеют характер градиентов (т-ры, концентрации и т.п.), в прерывных - конечных разностей этих величин.

Неравновесные процессы принято подразделять на скалярные, векторные и тензорные, если потоки и силы являются соотв. скалярами, векторами или тензорами. В зависимости от этого для описания процессов нужно использовать скалярное, векторное поле или поле тензора 2-го ранга. К группе скалярных процессов относят, в частности, хим. р-ции (скорость р-ции в каждой точке внутри системы характеризуется скалярной величиной). К векторным процессам относят, напр., теплопроводность и диффузию (с ними связаны поля векторов потоков тепла и в-ва). Примером тензорного процесса служит вязкое течение. Классификация процессов по тензорным св-вам не является формальной, но связана с содержанием принципа Кюри (см. ниже). Ур-ния балансов массы, импульса, полной энергии имеют смысл законов сохранения. Баланс внутр. энергии суть первое начало термодинамики. Его можно представить в виде ур-ния:

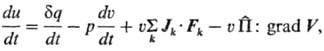
где и, u, q- уд. локальные (относящиеся к нек-рому выделенному элементу объема) внутр. энергия, объем и кол-во тепла соотв.; p -давление; J_k- диффузионный поток k -го компонента в поле внеш. силы F_k, действующей на единицу массы k -го компонента (точка означает скалярное произведение); V -вектор скорости центра масс системы в поле внутр. напряжений; П-тензор вязких напряжений (вязкий тензор давления); 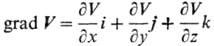(двоеточие означает двукратную свертку). Для невязких систем в поле сил тяготения последние два слагаемых обращаются в нуль, и приведенная формулировка первого начала аналогична формулировкам, принятым в равновесной термодинамике.

Поиск по сайту: