Произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку

Вопрос

Момент инерции сплошного диска (или цилиндра) относительно оси симметрии диска (цилиндра).

Разобьем диск на бесконечно тонкие кольца. Момент инерции отдельного кольца выражается так: dm r2,
где dm - масса кольца, r - его радиус.
Тогда момент инерции диска находится интегpиpованием:

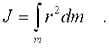
Чтобы вычислить интеграл, введем поверхностную плотность диска:

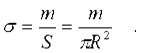
Тогда элементарную массу кольца можно выразить следующим образом:

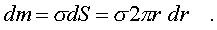
Теперь можно вычислить момент инерции диска:

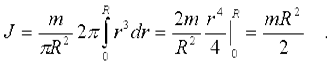
Вопрос

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

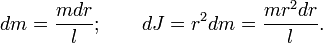
Интегрируя, получим

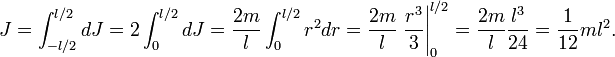
Вопрос

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

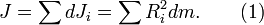
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

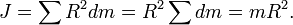
Вопрос

Вопрос

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

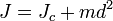
Если 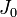— момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии 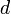от неё, равен

,

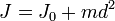где 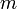— полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

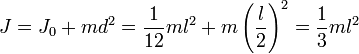
Вопрос

Кинетическая энергия вращающегося тела.

Моментом инерции мат.т. наз. физ. величина численно равная произведению массы мат.т. на квадрат расстояния этой точки до оси вращения.W_ki =m_iV²_i/2 V_i -Wr_i Wi=miw²r²_i/2 =w²/2*m_ir_i² I_i=m_ir²_i момент инерции твердого тела равен сумме всех мат.т I=S_im_ir²_i моментом инерции твердого тела наз. физ.величина равная сумме произведений мат.т. на квадраты расстояний от этих точек до оси. W_i-I_iW²/2 W_k=IW²/2

W_k =S_iW_ki момент инерции при вращательном движении явл. аналогом массы при поступательном движении. I=mR²/2

Вопрос

Моментом импульса т. наз. величина физически равная векторному произведению радиуса вектора т. на ее импульс L=[r*p] p=mV L=[r*mV] L=Iw lw –напр. в одну сторону.

Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

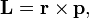
где 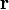— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, 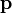— импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Закон сохранения момента импульса:
Если на систему вращающихся вокруг оси тел не действуют моменты внешних сил (система в этом смысле замкнута) или внешние моменты взаимно уравновешиваются, то суммарный момент импульса системы относительно оси вращения с течением времени не изменяется.
Таким образом, закон утверждает, что внутренние моменты сил системы не в состоянии изменить полный суммарный момент импульса системы тел, а в состоянии лишь перераспределить его. Внутри системы возможна лишь передача момента импульса от тела к телу.
В аналитическом виде закон сохранения момента импульса записывается следующим образом: если Mвнеш = 0, то

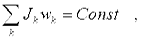
или так: для начального и конечного момента времени

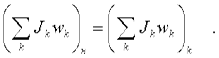
Вопрос

Принцип относительности Галилея – это принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы.

Математически принцип относительности Галилея выражает инвариантность (неизменность) уравнений механики относительно преобразований координат движущихся точек (и времени) при переходе от одной инерциальной системы к другой — преобразований Галилея.
Пусть имеются две инерциальные системы отсчёта, одну из которых, S, условимся считать покоящейся; вторая система, S', движется по отношению к S с постоянной скоростью u так, как показано на рисунке. Тогда преобразования Галилея для координат материальной точки в системах S и S' будут иметь вид:
x' = x - ut, у' = у, z' = z, t' = t (1)
(штрихованные величины относятся к системе S', нештрихованные — к S). Т. о., время в классической механике, как и расстояние между любыми фиксированными точками, считается одинаковым во всех системах отсчёта.
Из преобразований Галилея можно получить соотношения между скоростями движения точки и её ускорениями в обеих системах:
v' = v - u, (2)
a' = a.
В классической механике движение материальной точки определяется вторым законом Ньютона:
F = ma, (3)
где m — масса точки, a F — равнодействующая всех приложенных к ней сил.
При этом силы (и массы) являются в классической механике инвариантами, т. е. величинами, не изменяющимися при переходе от одной системы отсчёта к другой.
Поэтому при преобразованиях Галилея уравнение (3) не меняется.
Это и есть математическое выражение Галилеева принципа относительности.

ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ.

В кинематике все системы отсчета равноправны между собой и движение можно описывать в любой из них. При исследовании движений иногда приходится переходить от одной системы отсчета (с координатной системой ОХУZ) к другой - (О`Х`У`Z`). Рассмотрим случай, когда вторая система отсчета движется относительно первой равномерно и прямолинейно со скоростью V=соnst.

Для облегчения математического описания предположим, что соответствующие оси координат параллельны друг другу, что скорость направлена вдоль оси Х, и что в начальный момент времени (t=0) начала координат обеих систем совпадали друг с другом. Используя справедливое в классической физике допущение об одинаковом течении времени в обеих системах, можно записать соотношения, связывающие координаты некоторой точки А(х,у,z) и А (х`,у`,z`) в обеих системах. Такой переход от одной системы отсчета к другой носит название преобразований Галилея):

ОХУZ О`Х`У`Z`

t = t` t`= t

х = х` + V<sub>x</sub>t х` = х - V_xt

y = y` y`= y

z = z` z` = z

_x = v`<sub>x</sub> + V<sub>x</sub> v`_x = v_x - V_x

a_x = a`<sub>x</sub> a`_x = a_x

Ускорение в обеих системах одинаково (V=соnst). Глубокий смысл преобразований Галилея будет выяснен в динамике. Преобразование скоростей Галилея отражает имеющий место в классической физике принцип независимости перемещений.

Сложение скоростей в СТО

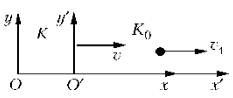Классический закон сложения скоростей не может быть справедлив, т.к. он противоречит утверждению о постоянстве скорости света в вакууме. Если поезд движется со скоростью v и в вагоне в направлении движения поезда распространяется световая волна, то ее скорость относительна Земли все равно c, а не v + c.

Рассмотрим две системы отсчета.

В системе K ₀ тело движется со скоростью v ₁. Относительно же системы K оно движется со скоростью v ₂. Согласно закону сложения скоростей в СТО: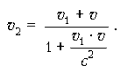

Если v << c и v ₁ << c, то слагаемым 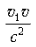можно пренебречь, и тогда получим классический закон сложения скоростей: v ₂ = v ₁ + v.

При v ₁ = c скорость v ₂ равна c, как этого требует второй постулат теории относительности: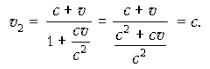

При v ₁ = c и при v = c скорость v ₂ вновь равна скорости c.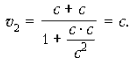

Замечательным свойством закона сложения является то, что при любых скоростях v ₁ и v (не больше c), результирующая скорость v ₂ не превышает c. Скорость движения реальных тел больше, чем скорость света, невозможна.

Сложение скоростей

При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.

Классическая механика

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

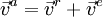
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.

Неинерциа́льная систе́ма отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, покоится либо движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того, чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции.

Вопрос

Статистической физикой называется раздел физики, посвященный изучению свойств макроскопических тел, исходя из свойств образующих тело частиц и взаимодействий между ними.

Статистический метод составляет основу молекулярной физики, это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними значениями физических величин, характеризующих всю совокупность частиц (например, средние значения скоростей теплового движения молекул и их энергий).

Термодинамический метод исследования - метод, использующий законы (начала) ТД и следствия из них (ТД построена дедуктивно: следствия, частные выводы получены из двух законов). Существует другой подход - статистический, в основе которого лежит молекулярно-кинетическая теория, квантовая механика и т.д.

При термодинамическом методе исследования не рассматривается внутреннее строение изучаемых тел, а анализируются условия и количественные соотношения при различных превращениях энергии, происходящих в системе.

Раздел физики, в котором физические свойства макроскопических систем изучаются с помощью термодинамического метода, называется термодинамикой.

Заметим, что статистическая физика и термодинамика при малом числе частиц теряют смысл.

Термодинамика имеет дело с термодинамической системой - совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией, как между собой, так и с другими телами (внешней средой).

Состояние системы задается термодинамическими параметрами (параметрами состояния). Обычно в качестве параметров состояния выбирают: - объем V, м³; давление Р, Па, (Р=dF_n /dS, где dF_n - модуль нормальной силы, действующей на малый участок поверхности тела площадью dS, 1 Па=1 Н/м²); термодинамическую температуру Т, К (Т=273.15 +t). Отметим, что термодинамическая температура прежде именовалась абсолютной температурой.

Понятие температуры, строго говоря, имеет смысл только для равновесных состояний.

Под равновесным состоянием понимают состояние системы, у которой все параметры состояния имеют определенные значения, не изменяющиеся с течением времени.

Параметры состояния, термодинамические параметры — физические величины, характеризующие состояние термодинамической системы: температура, давление, удельный объём, намагниченность, электрическая поляризация и др. Различают экстенсивные параметры состояния, пропорциональные массе системы:

объём, внутренняя энергия, энтропия, энтальпия, энергия Гиббса, энергия Гельмгольца (свободная энергия),

и интенсивные параметры состояния, не зависящие от массы системы: давление, температура, концентрация, магнитная индукция и др.

Вопрос

Не все параметры состояния независимы, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния.

Равновесный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.

Примеры равновесных процессов

Изотермический процесс, при котором температура системы не изменяется (T=const)

Изохорный процесс, происходящий при постоянном объёме системы (V=const)

Изобарный процесс, происходящий при постоянном давлении в системе(P=const)

T-const-изотермический P=const-изобарный V=const-изохорный

Вопрос

Основное уравнение молекулярно-кинетической теории идеального газа

Это уравнение связывает макропараметры системы – давление p и концентрацию молекул 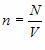с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:

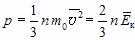
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки.

Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой.

Учитывая связь между концентрацией молекул в газе и его плотностью ( = nm ₀), можно получить еще одну форму основного уравнения МКТ идеального газа:

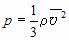
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)

В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния:

pV = vRT

где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная, 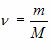, где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:

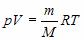
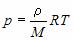
Пользуясь уравнением состояния, можно выразить один параметр через другой и построить график первого из них, как функции второго.

Графики зависимости одного параметра от другого, построенные при фиксированных температуре, объеме и давлении, называют соответственно изотермой, изохорой и изобарой.

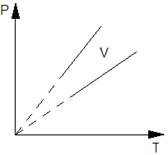
Например, зависимость давления p от температуры T при постоянном объеме V и постоянной массе m газа – это функция 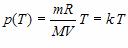, где k – постоянный числовой множитель. Графиком такой функции в координатах p,Т будет прямая, идущая от начала координат, как и графиком функции y(x)=kx в координатах y,x (рис. 3).

Зависимость давления p от объема V при постоянной массе m газа и температуре T выражается так:

,

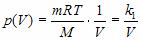где k ₁ – постоянный числовой множитель. График функции 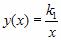в координатах y,x представляет собой гиперболу, так же как и график функции 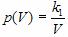в координатах p,V.

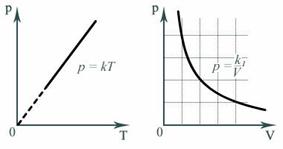
Рис. 3

Вопрос

Температура, как мера средней кинетической энергии молекул

Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ.

Введем понятие средней кинетической энергии молекул:

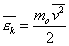(1)

Преобразуем основное уравнение МКТ с учетом формулы (1):

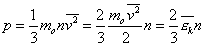т.е. основное уравнение МКТ запишем так 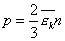(2)

Воспользуемся уравнением К.-М. в таком виде:

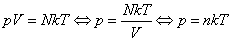(3)

Сравним уравнения (2) и (3) и получим, что

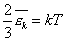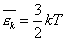или (4)

Как понимать формулу (4)?

Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура - мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества.

Молекулярно – кинетическое толкование абсолютной температуры.

C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <ε_k>хаотического движения молекул (T~<ε_k>).

Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <ε_k>=3/2kT где k - постоянная Больцмана, k=1.38*10^-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.

Формула позволяет выяснить смысл абсолютного нуля: T=0, если < ε_k > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.

Вопрос

Число степени свободы молекул. Закон равномерного распространения энергии по степеням свободы молекул.

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

показаны о 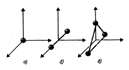дноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.

Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6).

В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT

закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы <ε>=i/2kT, где i - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=i_пост +i_вращ+2i_колеб.

В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то внутренняя энергия, отнесенная к одному молю газа, равна сумме кинетических энергий NA молекул: 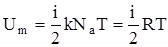.Внутренняя энергия для произвольной массы m газа 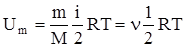, где k - постоянная Больцмана,  -количество вещества.

Функция распределения Максвелла – Больцмана характеризует распределение молекул по полным энергиям

Вопрос

Работа газа при изменении его объёма. Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

Если при изобарном расширении газа от объема V ₁ до объема V ₂ происходит перемещение поршня в цилиндре на расстояние l, то работа A', совершенная газом, равна

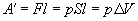
где p — давление газа, 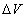— изменение его объема.

Количество теплоты — мера энергии, переходящей от одного тела к другому в данном процессе. Количество теплоты является одной из основных термодинамических величин.

Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.

Q=cmΔt, где Q- полученная телом теплота, c- удельная теплоемкость тела, Дж/(кг°С), m- масса тела, кг, Δt-изменение температуры тела, °С

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:

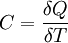
Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).

Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).

Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:

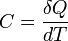
Вопрос

Первое начало термодинамики.

Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям. Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е. Q=∆U+A. В этом уравнении изменение внутренней энергии, Количество теплоты может быть положительным (Q>0), если тело получает теплоту, и отрицательным (Q>0), если тело отдает теплоту.

В дифференциальной форме это запишется следующим образом δQ=dU+δA

где dU и δA Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной.

Первое начало термодинамики и изопроцессы.

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат, где процесс 1-2 есть изохорное нагревание, а 1-3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.

.δA=pdV=0

Для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q=dU

DUm=CvdT. Тогда для произвольной массы газа получим Q=dU=mC_vT/M

Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V1 до V2 равна

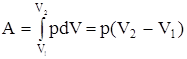и определяется площадью прямоугольника. Если использовать уравнение Клапейрона - Менделеева для выбранных нами двух состояний, то

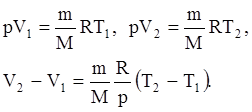
Тогда выражение для работы изобарного расширения примет вид

A=m/MR(T2-T1). Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-T1 =1 К, то для 1 моля газа R=А, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой m количества теплоты

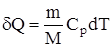его внутренняя энергия возрастает на величину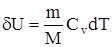

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля - Мариотта: PV=const.

Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Работа изотермического расширения газа:

.

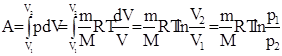Так как при T=const внутренняя энергия идеального газа не изменяется

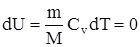то из первого начала термодинамики (Q=dU+A) следует, что для изотермического процесса Q=A, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил 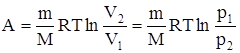Следовательно, для того, чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

Первое начало термодинамики и адиабатический процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики d Q = dU + dA для адиабатического процесса следует, что d A = – dU * т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выражения для элементарной работы и приращения внутренней энергии, для произвольной массы газа получаем уравнение в виде pdV=-m/MC_vdT Продифференцировав уравнение состояния для идеального газа pV=m/MRT, получим pdV+Vdp=m/mRdT Исключив из уравнений температуру Т:

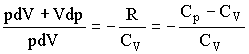
Разделив переменные и учитывая, что Cp/Cv = g, найдем dp/p=-γdV/V

Интегрируя это уравнение в пределах от р1 до р2 и соответственно от V1 до V2, а

затем потенцируя, придем к выражению p2/p1=(V₁/V₂) ^γ или p₁V₁^γ=p₂V₂^γ

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из полученного уравнения с помощью уравнения Клапейрона -Менделеева

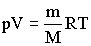соответственно давление или объем:TV^γ-1 = const T^γV^1-γ = const

Вопрос

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:

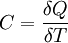
Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).

Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).

Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:

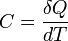
Выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина g = Cp/Cv = (i + 2)/I называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i = 3, g = 1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, g =1,4. Значения g, вычисленные по формуле (g = (i + 2)/i), хорошо подтверждаются экспериментом.

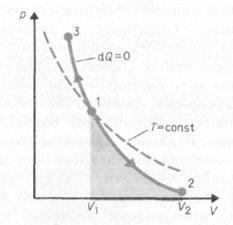
Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой. На рисунке видно, что адиабата (pVg = const) более крутая, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры в адиабатическом процессе. Запишем уравнение первое начало термодинамик для адиабатического процесса dA = – dU в виде

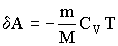Если газ адиабатически расширяется от объема Vl до V2, то его температура уменьшается от Т1 до Т2 и работа расширения идеального газа равна

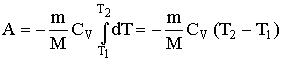
Работа, совершаемая газом при адиабатическом расширении 1 – 2 (численно равная площади под кривой), меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Поиск по сайту: