Вывод основного закона динамики вращательного движения

Вопрос

Материальная точка - тело, размерами которого в данных условиях движения можно пренебречь.

Абсолютно твердым телом называется тело, деформациями которого по условиям задачи можно пренебречь. У абсолютно твердого тела расстояние между любыми его точками с течением времени не меняется. В термодинамическом смысле такое тело не обязательно должно быть твердым. Произвольное движение твердого тела может быть разбито на поступательное и вращательное вокруг неподвижной точки.

Системы отсчёта. Чтобы описать механическое движение тела (точки), нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует, прежде всего, выбрать тело отсчёта и связать с ним систему координат. Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчёта времени. Система координат, тело отсчёта и указание начала отсчёта времени образуют систему отсчёта, относительно которой рассматривается движение тела. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчёта.

Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путём. Вектор, соединяющий начальную и конечную точки траектории называется перемещением. Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка. Промежуток времени считается достаточно малым, если скорость при неравномерном движении в течение этого промежутка не менялась. Определяющая формула скорости имеет вид v = s/t. Единица скорости — м/с. На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с). Измеряют скорость спидометром.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле a=Δv/Δt. Единица ускорения – м/с²

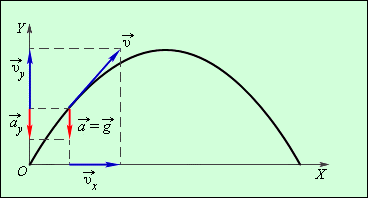
Рисунок 1.4.1. Проекции векторов скорости и ускорения 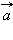на координатные оси. ax = 0, ay = – g

Если путь s, пройденный материальной точкой за промежуток времени t₂-t₁, разбить на достаточно малые участки D s_i, то для каждого i -го участка выполняется условие

Тогда весь путь можно записать в виде суммы

Сре́днее значе́ние — числовая характеристика множества чисел или функций; — некоторое число, заключённое между наименьшим и наибольшим из их значений.

- нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

- тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

Полное ускорение, с которым движется материальная точка, равно:

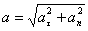
Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.

Следовательно

Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:

Вопрос

Кинематика вращательного движения.

Движение тела может быть как поступательным, так и вращательным. В этом случае тело представляется в виде системы жестко связанных между собой материальных точек.

При поступательном движение любая прямая, проведенная в теле, перемещается параллельно самой се­бе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения. Следовательно,скорости и ускорения всех точек тела в любой момент времени также одинаковы. Для описания поступательного движения достаточно определить движение одной точки.

Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой (ось вращения).

Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежа­щие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и, следовательно, имеют различные линейные скорости.

При вращении тела вокруг неподвижной оси точки тела за один и тот же промежуток времени совершают одно и тоже угловое перемещение . Модуль равен углу 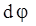поворота тела вокруг оси за время , направления вектора углового перемещения с направлением вращения тела связано правилом винта: если совместить направления вращения винта с направлением вращения тела, то вектор будет совпадать с поступательным движением винта. Вектор направлен вдоль оси вращения.

Быстроту изменения углового перемещения определяет угловая скорость - ω. По аналогии с линейной скоростью вводят понятия средней и мгновенной угловой скорости:

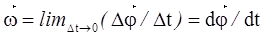
Угловая скорость - величина векторная.

Быстроту изменения угловой скорости характеризует среднее и мгновенное

угловое ускорение.

Вектор и может совпадать с вектором , и быть про­тивоположным ему

Вращательным наз. такой вид движения при котором каждая т. Твердого тела в процессе своего движения описывает окружность.У.с –наз.величина равная первой производной от угла поворота от времени W=dφ/dt физический смысл у.с. изменение угла поворота за единицу времени у.с. у всех т. Тела будет одинакова [1рад/с] Угловое ускорение(ε) –физическая величина числено равная изменению угловой скорости за единицу времени ε=dw/dt, W=dφ/dt ε=dw/dt=d²φ/dt связь. ε V=Wr a_t=dv/dt=d/dt(Wr)=r*dw/dt(ε) a_t=[ε*r] a_n = V²/r =W²*r²/r a_n=W²r

Линейная скорость показывает какой путь проходится за единицу времени при движении по окружности, линейное ускорение показывает на сколько изменяется линейная скорость в единицу времени. Угловая скорость показывает на какой угол перемещается тело при движении по окружности, угловое ускорение показывает на сколько изменяется угловая скорость в единицу времени. Vл = R*w; a = R*(бета)

Вопрос

Вследствие развития физики в начале XX века определилась область применения классической механики: ее законы выполняются для движений, скорость которых много меньше скорости света. Было установлено, что с ростом скорости масса тела возрастает. Вообще законы классической механики Ньютона справедливы для случая инерциальных систем отсчета. В случае неинерциальных систем отсчета ситуация иная. При ускоренном движении неинерциальной системы координат относительно инерциальной системы первый закон Ньютона (закон инерции) в этой системе не имеет места, – свободные тела в ней будут с течением времени менять свою скорость движения.

Первое несоответствие в классической механике было выявлено, тогда когда был открыт микромир. В классической механике перемещения в пространстве и определение скорости изучались вне зависимости от того, каким образом эти перемещения реализовывались. Применительно к явлениям микромира подобная ситуация, как выявилось, невозможна принципиально. Здесь пространственно-временная локализация, лежащая в основе кинематики, возможна лишь для некоторых частных случаев, которые зависят от конкретных динамических условий движения. В макро масштабах использование кинематики вполне допустимо. Для микро масштабов, где главная роль принадлежит квантам, кинематика, изучающая движение вне зависимости от динамических условий, теряет смысл.

Первый закон Ньютона

Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость постоянной, если на них не действуют другие тела и поля (или их действие взаимно скомпенсировано).

Массой тела называется количественная характеристика инертности тела. Масса - скал. величина, обл. свойствами:

-не зависит от скорости движ. тела

-масса – величина аддитивная, т.е. масса системы рана сумме масс мат. т., вход в состав этой системы

-при любых воздействиях выполняется закон сохранения массы: суммарная масса взаимодействующих тел до взаимодействия и после равны между собой.

Импульсом, или количеством движения мат.т. называется векторная величина p, равная произведению массы m мат. точки на её скорость. Импульс системы равен p=mV_c.

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу, как мерило проявления инерции материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Второй закон Ньютона утверждает, что

В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально приложенной к ней силе и обратно пропорционально её массе.
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где 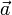— ускорение материальной точки; — сила, приложенная к материальной точке; m — масса материальной точки.

Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна действующей на неё силе.

где — импульс точки, где — скорость точки; t — время;

— производная импульса по времени.

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия.

Сам закон:

Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:

Сила тяготения

В соответствии с этим законом, два тела притягиваются друг к другу с силой, которая прямо пропорциональна массам этих тел m ₁ и m ₂ и обратно пропорциональна квадрату расстояния между ними:

Здесь r − расстояние между центрами масс данных тел, G − гравитационная постоянная, значение которой, найденное экспериментальным путем, составляет .

Сила гравитационного притяжения является центральной силой, т.е. направлена вдоль прямой, проходящей через центры взаимодействующих тел.

ВОПРОС

Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой

, (1)

где m – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.

Силой тяжести называется сила, действующая на любое находящееся вблизи земной поверхности тело.

Она определяется как геометрическая сумма действующей на тело силы гравитационного притяжения к Земле и центробежной силы инерции 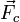, учитывающей эффект суточного вращения Земли вокруг собственной оси, т.е. . Направление силы тяжести является направлением вертикали в данном пункте земной поверхности.

НО величина центробежной силы инерции очень мала по сравнению с силой притяжения Земли (их отношение составляет примерно 3∙10^-3), то обычно силой 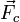пренебрегают. Тогда .

Вес тела

Вес тела – это сила, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес.

По третьему закону Ньютона обе эти силы упругости равны по модулю и направлены в противоположные стороны. После нескольких колебаний тело на пружине оказывается в покое. Это значит, что сила тяжести по модулю равна силе упругости F _упр пружины. Но этой же силе равен и вес тела.

Таким образом, в нашем примере вес тела, который мы обозначим буквой , по модулю равен силе тяжести:

.

Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости.

Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости F _упр.

Удлинение пружины пропорционально внешней силе и определяется законом Гука:

k – жесткость пружины. Видно, что чем больше k, тем меньшее удлинение получит пружина под действием данной силы.

Так как упругая сила отличается от внешней только знаком, т.е. F _упр = – F _вн, закон Гука можно записать в виде

,
F _упр = – kx.

Сила трения

Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.

Силами сухого трения называют силы, возникающие при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Они всегда направлены по касательной к соприкасающимся поверхностям.

Сухое трение, возникающее при относительном покое тел, называют трением покоя.

Сила трения покоя не может превышать некоторого максимального значения (F_тр)_max. Если внешняя сила больше (F_тр)_max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения и, вообще говоря, зависит от относительной скорости тел. Однако, во многих случаях приближенно силу трения скольжения можно считать независящей от величины относительной скорости тел и равной максимальной силе трения покоя.

Коэффициент пропорциональности μ называют коэффициентом трения скольжения.

Коэффициент трения μ – величина безразмерная. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей.

При движении твердого тела в жидкости или газе возникает сила вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя.

Сила вязкого трения сильно зависит от скорости тела. При достаточно малых скоростях F_тр ~ υ, при больших скоростях F_тр ~ υ². При этом коэффициенты пропорциональности в этих соотношениях зависят от формы тела.

Силы трения возникают и при качении тела. Однако силы трения качения обычно достаточно малы. При решении простых задач этими силами пренебрегают.

Внешние и внутренние силы

Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор.

Внешние силы делятся на объемные и поверхностные. Объемные силы при­ложены к каждой частице тела по всему его объему. Примером объемных сил являются силы веса и силы инерции. Поверхностные силы делятся на сосредоточенные и распределенные.
Сосре­доточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно счи­тать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в кН.
Распределенные нагрузки бывают распределенными по длине и по площади. Распределенные силы измеряются, как правило, в кН/м².

В результате действия внешних сил в теле возникают внутренние силы.
Внутренняя сила — мера взаимодействия между частицами одного тела.

Замкнутая система — термодинамическая система, которая не обменивается с окружающей средой ни веществом, ни энергией. В термодинамике постулируется (как результат обобщения опыта), что изолированная система постепенно приходит в состояние термодинамического равновесия, из которого самопроизвольно выйти не может (нулевое начало термодинамики).

ВОПРОС

Законы сохранения — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.

Некоторые из законов сохранения выполняются всегда и при всех условиях (например, законы сохранения энергии, импульса, момента импульса, электрического заряда), или, во всяком случае, никогда не наблюдались процессы, противоречащие этим законам. Другие законы являются лишь приближёнными и выполняющимися при определённых условиях.

Законы сохранения

В классической механике законы сохранения энергии, импульса и момента импульса выводятся из однородности/изотропности лагранжиана системы — лагранжиан (функция Лагранжа) не меняется со временем сам по себе и не изменяется переносом или поворотом системы в пространстве. По сути это означает то, что при рассмотрении некой замкнутой в лаборатории системы будут получены одни и те же результаты — вне зависимости от расположения лаборатории и времени проведения эксперимента. Другие симметрии лагранжиана системы, если они есть, соответствуют другим сохраняющимся в данной системе величинам (интегралам движения); например, симметрия лагранжиана гравитационной и кулоновской задачи двух тел приводит к сохранению не только энергии, импульса и момента импульса, но и вектора Лапласа — Рунге — Ленца.

Вопрос

Закон сохранения импульса является следствием второго и третьего законов Ньютона. Он имеет место в изолированной (замкнутой) системе тел.

Такой системой называется механическая система, на каждое из тел которой не действуют внешние силы. В изолированной системе проявляются внутренние силы, т.е. силы взаимодействия между телами, входящими в систему.

Центр масс — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Определение

Положение центра масс (центра инерции) в классической механике определяется следующим образом:

где — радиус-вектор центра масс, — радиус-вектор i -й точки системы,

— масса i -й точки.

.

Это уравнение движения центра масс системы материальных точек с массой, равной массе всей системы, к которой приложена сумма всех внешних сил (главный вектор внешних сил) или теорема о движении центра масс.

Реактивное движение.

Движение тела, возникающее вследствие отделения от него части его массы с некоторой скоростью, называют реактивным.
Все виды движения, кроме реактивного, невозможны без наличия внешних для данной системы сил, т. е. без взаимодействия тел данной системы с окружающей средой, а для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой. Первоначально система покоится, т. е. ее полный импульс равен нулю. Когда из системы начинает выбрасываться с некоторой скоростью часть ее массы, то (так как полный импульс замкнутой системы по закону сохранения импульса должен оставаться неизменным) система получает скорость, направленную в противоположную сторону. Действительно, так как m₁v₁+m₂v₂=0, то m₁v₁=-m₂v₂, т. е. v₂=-v₁m₁/m₂.

Из этой формулы следует, что скорость v₂, получаемая системой с массой m₂, зависит от выброшенной массы m₁ и скорости v₁ ее выбрасывания.

Тепловой двигатель, в котором сила тяги, возникающая за счет реакции струи вылетающих раскаленных газов, приложена непосредственно к его корпусу, называют реактивным. В отличие от других транспортных средств устройство с реактивным двигателем может двигаться в космическом пространстве.

Движение тел с переменной массой.

Уравнение Мещерского.

,
где v_отн- скорость истечения топлива относительно ракеты;
v - скорость движения ракеты;
m - масса ракеты в данный момент времени.

Формула Циолковского.

,
m₀ - масса ракеты в момент старта

Вопрос

Работа переменной силы

Пусть тело движется прямолинейно с равномерной силой под углом £ к направлению перемещения и проходит расстояние S/ Работой силы F называется скалярная физическая величина, равная скалярному произведению вектора силы на вектора перемещения. A=F·s·cos £. А=0, если F=0, S=0, £=90º. Если сила непостоянная (изменяется), то для нахождения работы следует разбивать траекторию на отдельные участки. Разбиение можно производить до тех пор, пока движение не станет прямолинейным, а сила постоянной │dr│=ds.. Работа, совершенная силой на данном участке определяется по представленной формуле dA=F· dS· cos £= = │F│·│dr│· cos £=(F;dr)=F_t·dS A=F·S· cos £=F_t·S. Таким образом, работа переменной силы на участке траектории равна сумме элементарных работ на отдельных малых участках пути A=SdA=SF_t·dS= =S(F·dr).

Работа переменной силы в общем случае вычисляется посредством интегрирования:

Мощностью (мгновенной мощностью) называется скалярная величина N, равная отношению элементарной работы dА к малому промежутку времени dt, в течение которого эта работа совершается.

®

Средней мощностью называется величина<N>, равная отношению работы А, совершаемой за промежуток времени D t, к продолжительности этого промежутка

Консервативная система — физическая система, работа неконсервативных сил которой равна нулю и для которой имеет место закон сохранения механической энергии, то есть сумма кинетической энергии и потенциальной энергии системы постоянна.

Примером консервативной системы служит солнечная система. В земных условиях, где неизбежно наличие сил сопротивления (трения, сопротивления среды и др.), вызывающих убывание механической энергии и переход её в другие формы энергии, например в тепло, консервативная система осуществляются лишь грубо приближённо. Например, приближённо можно считать консервативной системой колеблющийся маятник, если пренебречь трением в оси подвеса и сопротивлением воздуха.

Диссипативная система — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой.

Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве, то есть не выполнение Теоремы Лиувилля.

Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова — Жаботинского и сама биологическая жизнь.

Термин «диссипативная структура» введен Ильёй Пригожиным.

Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) системы сохраняется во времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую. Закон сохранения энергии встречается в различных разделах физики и проявляется в сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии называется первым началом термодинамики.

Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то правильнее называть его не законом, а принципом сохранения энергии.

Закон сохранения энергии является универсальным. Для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающихся для разных систем.

Согласно теореме Нётер, закон сохранения энергии является следствием однородности времени.

W=W_k+W_п=const

Вопрос

Кинетической энергией тела называется энергия его механического движения.

В классической механике

Кинетическая энергия механической системы

Изменение кинетической энергии механической системы равно алгебраической сумме работ всех внутренних и внешних сил, действующих на эту систему

или

Если система не деформируется, то

и

Кинетическая энергия механической системы равна сумме кинетической энергии поступательного движения ее центра масс и кинетической энергии той же системы в ее движении относительно поступательно движущейся системы отсчета с началом в центре масс W_к' (теорема Кёнига)

Потенциальная энергия. Рассмотрение примеров взаимодействия тел силами тяготения и силами упругости позволяет обнаружить следующие признаки потенциальной энергии:

Потенциальной энергией не может обладать одно тело, не взаимодействующее с другими телами. Потенциальная энергия — это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела — это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела — это энергия взаимодействия отдельных частей тела между собой силами упругости.

Механическая энергия частицы в силовом поле

Сумму кинетической и потенциальной энергии - называют полной механической энергией частицы в поле:

(5.30)

Заметим, что полная механическая энергия Е, как и потенциальная, определяется с точностью до прибавления несущественной произвольной постоянной.

Вопрос

Вывод основного закона динамики вращательного движения.

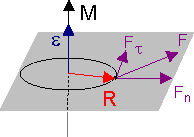
Рис. 8.5. К выводу основного уравнения динамики вращательного движения.

Динамика вращательного движения материальной точки. Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F (см. рис. 8.5). В инерциальной системе отсчета справедлив 2 ^ой закон Ньютона. Запишем его применительно к произвольному моменту времени:

F = m· a.

Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид:

F_t = m·a_t.

Поскольку a_t = e·R, то

F_t = m·e·R (8.6)

Умножив левую и правую части уравнения скалярно на R, получим:

F_t·R= m·e·R² (8.7)
M = I·e. (8.8)

Уравнение (8.8) представляет собой 2 ^ой закон Ньютона (уравнение динамики) для вращательного движения материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора углового ускорения, направленного вдоль оси вращения (см. рис. 8.5):

M = I· e. (8.9)

Основной закон динамики материальной точки при вращательном движении можно сформулировать следующим образом:

Поиск по сайту: