АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Разностные уравнения рекурсивных и нерекурсивных фильтров

Читайте также:
  1. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  2. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  3. V2: Применения уравнения Шредингера
  4. V2: Уравнения Максвелла
  5. VI Дифференциальные уравнения
  6. Алгебраические уравнения
  7. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  8. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  9. Вывод уравнения совершенного гидравлического прыжка.(стр11)
  10. Геометрическая оптика.отражение и преломление света. законы отражения и преломления.Зеркала и линзы.Уравнения для зеркал и линз.оптические приборы.
  11. Геометрический образ уравнения состояния.
  12. Гидролиз дисахаридов Фильтрование вытяжки

 

Важную роль в системах обработки сигналов играют рекурсивные фильтры 1-го и 2-го порядков.

• Базовый рекурсивный фильтр 1-го порядка. Базовым РФ 1-го порядка называют фильтр, описываемый разностным уравнением вида:

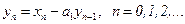(6)

Применив z-преобразование к левой и правой частям уравнения, получим

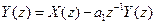. (7)

Следовательно, передаточная функция фильтра имеет вид

. (8)

• Рекурсивный фильтр 1-го порядка. Разностное уравнение имеет вид:

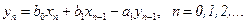(9)

Применив z-преобразование к левой и правой частям уравнения, получим

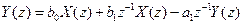. (10)

Отсюда

. (11)

 

• Базовый рекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная функция имеют вид:

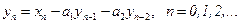(12)

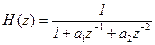. (13)

 

• Рекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная Функция имеют вид:

(14)

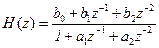. (15)

• Нерекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная функция имеют вид:

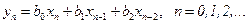(16)

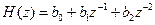. (17)

На основе приведенных примеров можно сформулировать мнемоническое правило определения передаточной функции по разностному уравнению (и наоборот):

• коэффициенты разностного уравнения являются коэффициентами передаточной функции;

• коэффициенты разностного уравнения 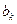при равны коэффициентам числителя передаточной функции при z-k, k = 0, 1,.... N -1.

• коэффициенты разностного уравнения bk при xn-k равны коэффициентам знаменателя передаточной функции (с обратным знаком) при z-k, k = О, 1,..., N~1.

Пример. Известна передаточная функция рекурсивного фильтра

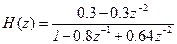. (18)

Разностное уравнение имеет вид:

(19)

• В общем случае передаточная функция дискретного фильтра может быть получена путем применения z-преобразования к разностным уравнениям (1) и (2). Рекурсивный фильтр:

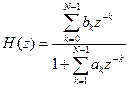(20)

Нерекурсивный фильтр:

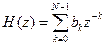(21)

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.507 сек.)