 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Важным понятием при представлении числовых данных является понятие системы счисления
Система счисления - это способ наименования и представления чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа представления чисел системы счисления делятся на позиционные и непозиционные.
В позиционных системах количественное значение каждой цифры зависит от места (позиции) в числе. В непозиционных системах цифры не меняют своего количественного значения при изменении их расположения в числе. Примером позиционной системы является арабская десятичная система (0 - 9). Римская система, в которой для каждого числа используется специфическое сочетание символов XХV=25, CХ=110 и т. д., является примером непозиционной системы счисления.
Алфавитом системы счисления называется набор элементарных символов, из комбинации которых образуются любые численные значения. Количество таких символов и определяет название системы счисления: двоичная – два (0 и 1); восьмеричная – восемь (0, 1, 2, 3, 4, 5, 6, 7, 8); десятичная – десять (0-9); шестнадцатеричная – шестнадцать (0-9, A, B, C, D, E, F).
Таблица 1.3 Представление чисел в различных системах счисления
| Система счисления | |||
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Общее правило перевода чисел из одной системы счисления в другую формулируется так: перевод числа Х из системы счисления основанием P в систему счисления с основанием К выполняется путем нахождения остатков от деления числа Х на основание К, при этом процесс продолжается до тех пор, пока частное от деления не будет меньше основания К. Все вычисления выполняются в системе счисления с основанием Р.
Например, для перевода числа 10 из десятичной системы счисления в двоичную необходимо найти остатки отделения числа 10 на 2 (иллюстрируется схемой). Аналогично выполняются преобразования в восьмеричную и шестнадцатеричную системы счисления.

Для обратного перевода числа из любой системы счисления в десятичную удобнее использовать другое правило, которое в общем виде формулируется так: перевод числа Х из системы счисления основанием К в систему счисления с основанием Р осуществляется путем представления числа Х по степеням основания К. Все вычисления выполняются в системе счисления с основанием Р, т. е. основание К и цифры исходного числа должны также быть выражены в системе счисления с основанием Р. Например, перевод двоичного числа 1010 в десятичную систему счисления выполняется представлением числа 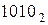 по степеням с основанием 2, начиная с нулевой степени при младшем (самом правом) разряде двоичного слова.
по степеням с основанием 2, начиная с нулевой степени при младшем (самом правом) разряде двоичного слова.
Эта процедура также проиллюстрирована схемой.
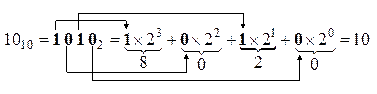
Перевод двоичного числа в восьмеричное и шестнадцатеричное числа выполняется по триадам и тэтрадам соответственно. В этом случае все двоичное слово разбивается на триады (три разряда) или тэтрады (четыре разряда) - соответственно справа
 |
налево.
Недостающие разряды в самой левой триаде (тэтраде) дополняются нулями. После этого выполняется преобразование двоичного числа в число соответствующей системы счисления с использованием их стандартного алфавита (таблица 1.3).
Поиск по сайту: