 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Выполнение 1-ой части курсовой работы. Расчет цепи постоянного тока
Рисунок 1.2.
1.Уравнения по законам Кирхгофа
Направление обхода контуров совпадает с направлением токов в ветвях дополнения, на рис. 1.2.

2. Определим токи во всех ветвях схемы:
а) методом контурных токов (контуры, определены ветвями дерева).

Подставим значения:
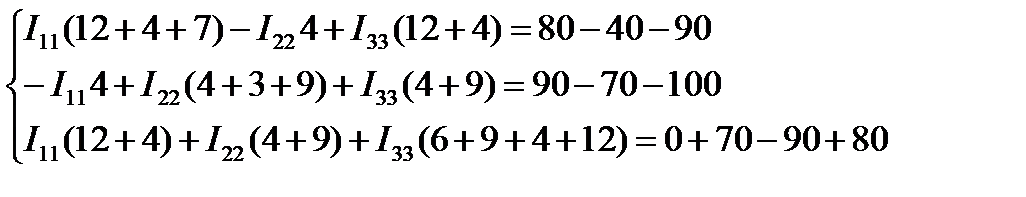
Преобразуем до вида:

Решим полученную систему уравнений методом Гауса.
| Матрица | своб ч. | ||||
| -4 | -50 | ||||
| -4 | -13 | -80 | |||
| -13 | |||||
| Прямой ход метода Гаусса: | |||||
| 1. Исключаем х1 из всех уравнений, начиная со второго | |||||
| -0,17391 | 0,695652 | -2,17391 | |||
| 15,30435 | -10,2174 | -88,6957 | |||
| -10,2174 | 19,86957 | 94,78261 | |||
| 2. Исключаем х2 из всех уравнений, начиная с третьего | |||||
| -0,17391 | 0,695652 | -2,17391 | |||
| -0,66761 | -5,79545 | ||||
| 13,0483 | 35,56818 | ||||
| 3. Последнюю строку делим на коэфф. | |||||
| -0,17391 | 0,695652 | -2,17391 | |||
| -0,66761 | -5,79545 | ||||
| 2,725887 | |||||
| 2. Этап. Обратный ход метода Гаусса. | |||||
| х3= | 2,72588722 | ||||
| х2= | -3,975615066 | ||||
| x1= | -4,76159373 |
Определяем токи в ветвях:

По первому закону Кирхгофа находим остальные токи:


б) методом узловых потенциалов. Потенциал узла 4 равен нулю.
Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по первому закону Кирхгофа.
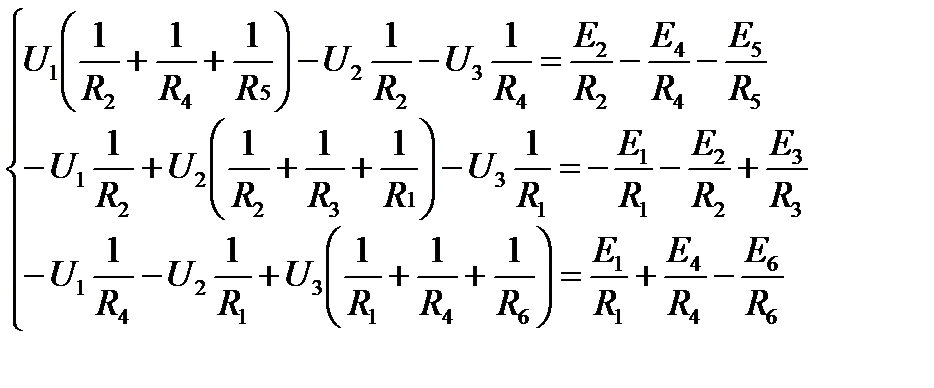
Подставим значения:

В матричном виде:
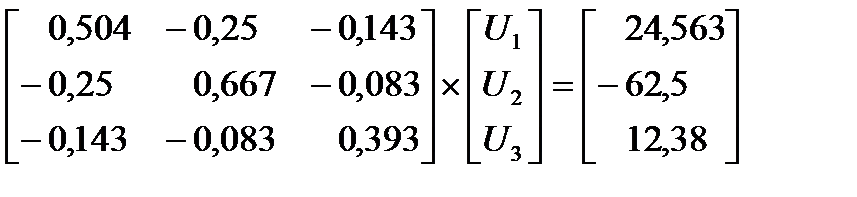
Решим полученную систему уравнений методом Крамера.
| Исходная матрица | Матр св. ч. | Опред исход | |||
| 0,504 | -0,25 | -0,143 | 24,563 | 0,084505485 | |
| -0,25 | 0,667 | -0,083 | -62,5 | ||
| -0,143 | -0,083 | 0,393 | 12,38 | ||
| Замена 1 | Опред 1 | ||||
| 24,563 | -0,25 | -0,143 | 0,824773526 | ||
| -62,5 | 0,667 | -0,083 | |||
| 12,38 | -0,083 | 0,393 | |||
| Замена 2 | Опред 2 | ||||
| 0,504 | 24,563 | -0,143 | -7,436119343 | ||
| -0,25 | -62,5 | -0,083 | |||
| -0,143 | 12,38 | 0,393 | |||
| Замена 3 | Опред 3 | ||||
| 0,504 | -0,25 | 24,563 | 1,391660593 | ||
| -0,25 | 0,667 | -62,5 | |||
| -0,143 | -0,083 | 12,38 | |||
| Х1 | Х2 | Х3 | |||
| 9,76 | -87,9957 | 16,468287 |
Используя полученные напряжения, находим токи по закону Ома для участка цепи содержащего ЭДС:
 (А)
(А)
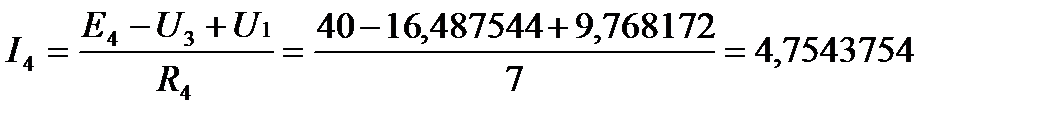 (А)
(А)








3. Определение тока в сопротивлении  методом эквивалентного генератора
методом эквивалентного генератора
Для того чтобы найти ток в сопротивлении  необходимо представить часть схемы в виде эквивалентного генератора (рисунок 1.3), найти ЭДС этого генератора равное напряжению холостого хода и его внутреннее сопротивление. Для этого преобразуем схему (рисунок 1.2) к виду (рисунок 1.4) и найдем токи.
необходимо представить часть схемы в виде эквивалентного генератора (рисунок 1.3), найти ЭДС этого генератора равное напряжению холостого хода и его внутреннее сопротивление. Для этого преобразуем схему (рисунок 1.2) к виду (рисунок 1.4) и найдем токи.
| I1 |
| RЭГ |
| R1 |
| E1 |
| EЭГ |
| UХХ |
Рисунок 1.3 Эквивалентный генератор
| Uхх |
| I5 |
| I6 |
| I4 |
| I3 |
| I2 |
| E6 |
| E5 |
| E2 |
| E3 |
| R6 |
| R5 |
| R4 |
| R3 |
| R2 |
Рисунок 1.4 Преобразованная схема
Найдем токи по методу контурных токов для контуров 1,3,4 и 1,2,4, направления обхода совпадают с токами на рисунке 1.4.

Подставим значения

В матричном виде

Решение матрицы приведено в приложении В.
Контурные токи и соответствующие им токи в ветвях равны:

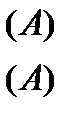
Тогда  находится по второму закону Кирхгофа:
находится по второму закону Кирхгофа:

Подставим значения:

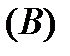
Находим ток короткого замыкания 
Для этого преобразуем схему (рисунок 1.2) к виду (рисунок 1.5).
| III |
| II |
| I |
| IКЗ |
| I6 |
| I4 |
| I3 |
| I2 |
| I1 |
| E6 |
| E2 |
| E3 |
| E1 |
| R6 |
| R4 |
| R1 |
| R3 |
| R2 |
Рисунок 1.5 Преобразованная схема
Найдем ток короткого замыкания по методу контурных токов:

Подставим значения:
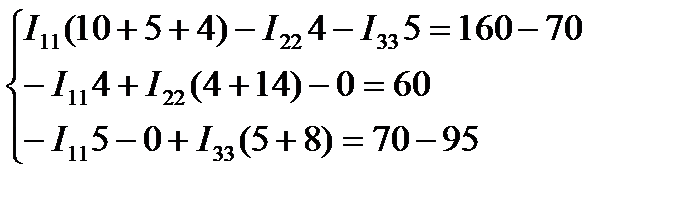
В матричном виде:

Решение матрицы приведено в приложении Г.
Контурные токи:

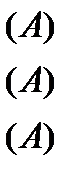
По первому закону Кирхгофа



Находим внутреннее сопротивление эквивалентного генератора:


Искомый ток в пятой ветви равен:


Поиск по сайту: