Простые проценты

Под наращенной суммойссуды (депозита, инвестированных средств, платежного обязательства и т.п.) понимается ее первоначальная сумма с начисленными на нее процентами к концу срока наращения.Величина наращенной суммы представляет собой произведение первоначальной суммы ссуды на множитель наращения, который показывает во сколько раз наращенная сумма больше первоначальной.В зависимости от применяемой процентной ставки и условий наращения формула расчета множителя наращения записывается по-разному.

Например, для наращения по простым процентам наращенная сумма (S) будет рассчитываться так:

,

где Р – первоначальная сумма ссуды, ден. ед.; п –срок ссуды (а днях, месяцах, годах и т. п.); i – ставка наращения (простая постоянная), ед.

Выражение (1 + ni) называется множителем наращения.

В финансово-экономических расчетах срок ссуды обычно измеряется годами, поэтому значение ставки наращения i есть значение годовой ставки процентов. Проценты, начисленные за весь срок ссуды, в этом случае составят:

,

где I – процентная сумма (величина дохода), ден. ед.

Представленная выше формула называется формулой простых процентов, а величину I можно определить как процентный доход, или процентные деньги (проценты).

В практической работе банки, коммерческие организации, финансовые институты и т.п. используют различные способы изменения числа дней ссуды (t) и продолжительности года ( временной базыдля расчета процентов) в днях (К).В зависимости от того, как определяются величины t и К– точно, или приблизительно применяются следующие варианты («практики», «системы») начисления простых процентов.

1. Точные проценты с фактическим числом дней ссуды(так называемая «английская» практика).Этот вариант дает самые точные результаты и применяется многими центральными и крупными коммерческими банками мира. В этом случае K=365 дням, а в месяцах 28, 29, 30 и 31 день.

2. Обыкновенные проценты с точным числом дней ссуды(так называемая «французская»практика или банковский метод).Этот вариант дает несколько больший результат, чем применение точных процентов.Так, если число дней ссуды превышает 360, то данный способ измерения времени приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, при t = 363 дням, n=363:З60=1,0083, а множитель наращения за этот период будет равен: 1+1,0083*i.

3.Обыкновенные проценты с приближенным числом днейссуды («германская»практика). Подсчет числа дней в этом варианте базируется на годе в 360 дней и месяцах по 30 дней. Поскольку точное число дней ссуды в большинстве случаев больше приближенного, то проценты с точным числом дней обычно больше, чем с приближенным, a следовательно, и наращенная сумма по процентам с точным числом дней обычно выше.

Наращение суммы в случае изменения простой процентной ставки в течение срока ссуды.На практике часто встречается ситуация, когда кредитные договоры (соглашения) предусматривают изменение процентной ставки в течение срока ссуды (например, в связи с изменением ставки рефинансирования; желанием банка учесть темп инфляции и т. д.). При этом годовая ставка процентов, указанная в кредитном договоре, носит название номинальной.В этом случае наращенная сумма будет исчисляться следующим образом:

,

где i_t, – ставка простых процентов в периоде t; t=l,2,...,m; ед.;

n_t, – продолжительность периода; лет;

т – число периодов, ед.

Наращение суммы при реинвестировании.В целях повышения заинтересованности вкладчиков и быстрого привлечения дополнительных денежных средств, например, в кратко- и среднесрочные депозиты, банки и финансовые компании могут предлагать производить своим клиентам неоднократное наращение вложенной суммы в пределах общего срока займа, т.е. реинвестировать ее. Иными словами, реинвестирование предполагает присоединение начисленных процентов к исходной (первоначальной) сумме и начисление процентов уже на возросшую сумму, и так несколько раз за период.При таком реинвестировании наращенная сумма рассчитывается по формуле:

,

где n₁,n₂,...n_t – продолжительность периодов наращения, лет;

причем (общий срок сделки);

i₁, i₂, … i_t, – ставки реинвестирования, ед.

В частном случае, когда и 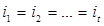, т.е. когда периоды начисления и ставки процентов равны формула принимает

,

где m – число операций реинвестирования, ед.

Пример 1.1.На сумму вклада в размере 50 тыс. р. в течение месяца начисляются простые проценты по ставке 24% годовых. Какова будет наращенная сумма, если эта операция будет повторена в течение 6 мес. текущего года (т.е. при реинвестировании этой суммы шесть раз) при расчете точных процентов с фактическим числом дней ссуды с 1 -го марта?

Решение.

По условиям примера Р = 50 тыс. р.; i = 0,24. Точное число дней не високосного года, начиная с марта и заканчивая августом составит: 31+30+31+30+31->-31=184 дня.

По формуле получаем:

Пример 1.2.Потенциальный клиент ряда надежных и расположенных в пределах его пешеходной доступности банков города имеет временно свободные денежные средства в размере 10 тыс. р. и хотел бы поместить их на депозитный счет сроком на 1 год. Первый банк (банк А) предлагает ему сделать вклад на условиях ежеквартального начисления по ставке 20% годовых и капитализации (реинвестирования) процентов. Второй банк (банк Б) на следующих условиях: начисление на вклад по ставке 24% годовых дважды в год с капитализацией процентов. Банк В предлагает ежемесячное начисление процентов по ставке 20% годовых и капитализацией начисленных процентов. И, наконец, банк Г предлагает сделать вклад на условиях начисления 25% годовых без капитализации процентов и начисления их в конце срока вклада.

В каком из банков вкладчик может получить наибольшую сумму по окончании срока договора?

Решение.

По условиям примера Р = 10тыс. р.; i₁ = 20%; i₂ = 24%; i₃ = 20%; i₄ = 25%. Учитывая, что начисление процентов происходит ежеквартально, по полугодиям и ежемесячно с капитализацией, и только в банке Г – в конце года (без реинвестирования), по формуле и получим (тыс. р.):

;

;

;

.

Наращенная сумма при вкладах в конце и в начале каждого года.

Довольно часто по условиям договоров вклада депозитных договоров банки предусматривают возможность довложения определенной (часто – не выше первоначальной) денежной суммы.

В случае если вклады делаются в конце каждого года, то наращенная сумма составит:

,

где m – число вкладов, ед.; D – величина вклада, ден. ед.

Если вклады по своей величине равны, т.е. D₁=D₂=D₃=D_m, _То формулу можно записать так:

,

или, учитывая, что

,

можно окончательно написать:

.

Очевидно, что наращение по ставке простых процентов в случае, когда довложения делаются в начале года, существенно выгоднее по сравнению в довложениями в конце года.Это происходит потому, что в первом случае увеличивается на один год наращения.

Расчет суммы необходимого депозита при ежегодных выплатах. Довольно часто (особенно при работе с клиентами – пенсионерами, со вкладами на несовершеннолетних и т.п.) работники банка, работающие со вкладами населения, сталкиваются с задачей определения необходимой первоначальной суммы вклада (депозита) клиента, который смог бы обеспечить ему определенные ежегодные выплаты в течении n лет по заранее оговоренной ставке процентов. В общем случае эта задача сводится к решению задачи определения «вечной» ренты, которая подробно будет рассмотрена ниже. Сейчас же рассмотрим ее решение исходя из тех знаний, которые мы уже имеем.

Используя формулу , можно составить следующее уравнение:

,

где Р₁,Р₂,…,Р_n – определенные ежегодные выплаты, ден, ед.; п – время выплат, лет.

При условии равенства ежегодных выплат, т.е. при P₁ =P₂ = Р₃ = Рn формулу можно преобразовать в выражение следующего вида:

.

Для приближенных, оценочных расчетов величины первоначального вклада можно использовать примерное равенство выражений:

.

Пример 1.3.Рассчитать необходимую первоначальную величину депозита клиента для того, чтобы он имел возможность ежегодно в течении 5 лет получать со своего счета в банке сумму в размере 6 тыс. руб. при начислении простой процентной ставки, равной 30% годовых.

Решение

По условиям примера Р=6 тыс. руб.; i_n=30%; n=5 лет. Используя формулу , получим (тыс. р.):

.

Расчет по формуле дает следующий результат:

.

Расхождение по сравнению с результатом, полученным по первой формуле, равно – 0,046 тыс. руб., или менее 0,3%. Как видим, расчет по второй формуле дает вполне приемлемый результат.

Расчет срока ссуды и уровня процентной ставки.При подготовке обоснования для получения ссуды и расчета ее эффективности возникает задача определения срока ссуды и уровня процентной ставки при имеющихся прочих условиях. В этом случае срок ссуды может быть определен как в годах, так и в днях:

в годах ;

в днях .

Соответственно и размер процентной ставки может быть определен при исчислений срока ссуды в годах как:

,

а при исчислении срока ссуды в днях так:

.

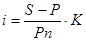Наращение и равномерная выплата процентов в потребительском кредите. В потребительском кредите, т.е. кредите, как правило, на личные нужды для приобретения товаров (или услуг) проценты начисляются на всю сумму кредита и присоединяются к основному долгу чаще всего уже в момент открытия кредита. Такой подход называется разовым начислением процентов, апогашение долга с процентами в этом случае производится обычно равными суммами на протяжении всего срока кредита. Наращенная сумма долга при таком подходе рассчитывается по формуле , а величина разового погасительного платежа (R) так:

,

где т – число погасительных платежей по кредиту в году, ед.

Заметим, что в связи с тем, что проценты начисляются на первоначальную сумму долга, а фактическая его величина постоянно уменьшается со временем, действительная процентная ставка (по фактически использованному кредиту) оказывается заметно выше, чем ставка по первоначальным договорным условиям.

Вопросы для самопроверки:

1. Что является предметов финансовой математики?

2. Какую роль играет время в финансовых расчетах?

3. Перечислите виды процентных ставок.

4. Что такое наращенная сумма?

5. Что такое дисконтирование?

6. Как определяется величина процентной ставки?

7. Как рассчитывается срок ссуды.

Поиск по сайту: