АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Эти параметры рассматриваются при дискретных и непрерывных процентах

Читайте также:
  1. Базовые параметры радиационных свойств горных пород и методы их определения
  2. Базовые параметры электромагнитных свойств горных пород и методы их определения.
  3. Балльная оценка параметров инвестиционной привлекательности организаций и первичные параметры оценки. Метод интегральной оценки.
  4. Виды линий связи и их электрические параметры
  5. Визуальные параметры видео-дисплейных терминалов, контролируемые на рабочих местах
  6. Воздухопроницаемость материалов и ОК в целом: отличия параметры и закономерности. Температурный расчет ОК в условиях воздухопроницания.
  7. Вопрос№15 Механические колебания. Виды колебаний. Параметры колебаний движения
  8. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
  9. Вычисление непрерывных случайных величин.
  10. ГЛАВА 3 ТРЕНИРОВОЧНАЯ НАГРУЗКА И ЕЕ ПАРАМЕТРЫ
  11. Диагностирование дискретных устройств с памятью. Построение диагностических и проверяющих тестов
  12. ДИАГНОСТИЧЕСКИЕ ПАРАМЕТРЫ

С помощью этих формул можно ответить на вопрос, например, ч то выгоднее: увеличение вклада в три раза за три года или 46% годовых? Ответ: увеличение вклада за три года в три раза эквивалентно годовой процентной ставке в 44,3%, поэтому размещение денег под 46% годовых будет более выгодно.

Дисконтирование по сложным процентам осуществляется по формуле:

.

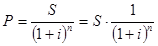При определении первоначальной суммы, необходимой для покрытия потока будущих платежей в течение n лет пользуются формулой:

.

Формулу можно преобразовать с учетом формулы суммы n членов геометрической прогрессии.

При вложениях, равных первоначальной сумме пользуются формулами:

1. в начале каждого года:

.

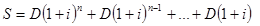2. в конце каждого года:

.

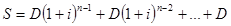Формулы также можно преобразовать с учетом формулы суммы n членов геометрической прогрессии.

Наращенная сумма для довложений в начале года в 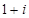раза больше, чем для довложений в конце.

Вопросы для самопроверки:

1. В чем отличие сложных процентов от простых?

2. В каких случаях целесообразно применение сложных процентов?

3. Что такое множитель наращения? В чем заключается его экономический смысл?

4. Какую процентную ставку называют силой роста?

5. Перечислите виды начисления процентов в зависимости от частоты начисления.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)