Комплект заданий для контрольной работы№ 2

Комплект заданий для контрольной работы №1

по дисциплине __ Математика_(2 семестр)_________________

^{(наименование дисциплины)}

Тема: Интегральное исчисление функций одной переменной. Обыкновенные дифференциальные уравнения

Вариант 1

1. Вычислить неопределенный интеграл:

а) ; б)

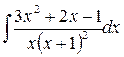
2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

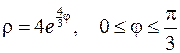6. Решить дифференциальные уравнения

1. y′ = 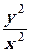+ 4 + 2

2. y′ – = x², y(1) = 0

3. y′′′ x ln x = y′′

4. y”+2y’=4e^x(sinx+cosx)

Вариант 2

1. Вычислить неопределенный интеграл:

а) ; б)

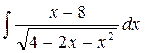
2. Вычислить определенный интеграл:

а) ; б)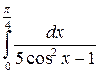

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

6. Решить дифференциальные уравнения

1. x y′ =

2. y′ – y ctg x = 2x sinx, y(π/2) = 0

3. xy′′′ + y′′ = 1

4. y”+2y’=-2e^x(sinx+cosx)

Вариант 3

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенные интегралы:

а) 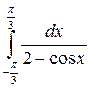; б)

3. Найти несобственный интеграл или доказать его расходимость:

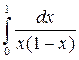
4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями: .

6. Решить дифференциальные уравнения

1. y′ =

2. y′ + y cos x = sin 2x, y(0) = 0

3. 2xy′′′ = y′′

4. y”+2y’+5y=-sin2x

Вариант 4

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенные интегралы:

а) ; б)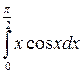

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

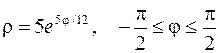6. Решить дифференциальные уравнения

1. xy′ = + y

2. y′ +y tg x = cos² x, y(π/4) = ½

3. xy′′′ + y′′ = x + 1

4. y”+2y’=e^x(sinx+cosx)

Вариант 5

1. Вычислить неопределенный интеграл:

а) 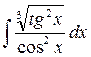; б)

2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

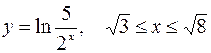5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

6. Решить дифференциальные уравнения

1. 2y′ = 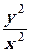+ 6 + 3

2. y′ – = x² + 2x, y(-1) = 3/2

3. tg x y′′ – y′ + = 0

4. y’’+6y’+13y= e^-3xcos4x

Вариант 6

1. Вычислить неопределенный интеграл:

а) ; б) ;

2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

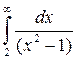
4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

6. Решить дифференциальные уравнения

1. xy′ =

2. y′ – y = e^x (x + 1), y(0) = 1

3. x² y′′ + xy′ = 1

4. y”+2y’=10e^x(sinx+cosx)

Вариант 7

1. Вычислить неопределенный интеграл:

а) ; б)

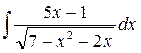
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

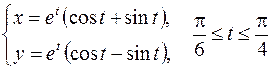6. Решить дифференциальные уравнения

1. y′ =

2. y′ – = x sin x, y(π/2) = 1

3. y′′′ ctg 2x + 2y′′ = 0

4. y”+y=2cos5x+3sin5x

Вариант 8

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенные интегралы:

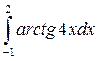
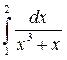
3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, заданной уравнением:

.

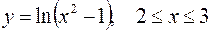5. Вычислить длину дуги, заданной уравнением:

.

6. Решить дифференциальные уравнения

1. xy′ = 2 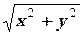+ y

2. y′ + = sinx, y(π) = 1/π

3. x³ y′′′ + x² y′′ = 1

4. y”+6y’+13y=e^-3xcosx

Вариант 9

1. Вычислить неопределенный интеграл:

а) ; б) ;

2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

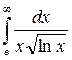
4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

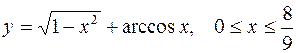5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

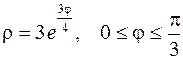6. Решить дифференциальные уравнения

1. 3y′ = 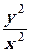+ 8 + 4

2. y′ + 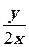= x², y(1) = 1

3. tg x y′′′ = 2y′′

4. y”+2y’+5y=-2sinx

Вариант 10

1. Вычислить неопределенный интеграл:

а) 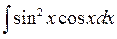; в)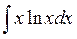

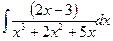
2. Вычислить определенные интегралы:

а) ; б)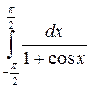

3. Найти несобственный интеграл или доказать его расходимость:

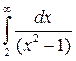
4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

6. Решить дифференциальные уравнения

1. xy′ =

2. y′ + y = , y(0) = 2/3

3. x⁴ y′′ + x³ y′ = 1

4. y”+2y’=6e^x(sinx+cosx)

Вариант 11

1. Вычислить неопределенный интеграл:

а) ; б) ;

2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

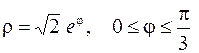6. Решить дифференциальные уравнения

1. y′ =

2. y′ – y = 5, y(2) = 4

3. xy′′′ + 2y′′ = 0

4. y”+6y’+13y= e^-3xcos5x

Вариант 12

1. Вычислить неопределенный интеграл:

а) ; б)

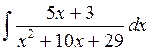
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

6. Решить дифференциальные уравнения

1. x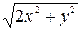y′ = + y

2. y′ + = e^x, y(1) = e

3. (1 + x²)y′′ + 2xy′ = x³

4. y”+2y’+5y=-cosx

Вариант 13

1. Вычислить неопределенный интеграл:

а) ; б)

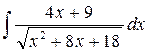
2. Вычислить определенные интегралы:

а) 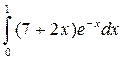; б)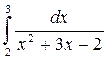

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

6. Решить дифференциальные уравнения

1. y′ = 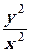+ 6 + 6

2. y′ – = - , y(1) = 1

3. x⁵ y′′′ + x⁴ y′′ = 1

4. y”+6y’+13y== e^-3xcos8x

Вариант 14

1. Вычислить неопределенный интеграл:

а) 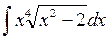; б)

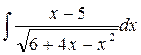
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

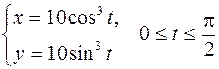6. Решить дифференциальные уравнения

1. xy′ =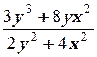

2. y′ – = - , y(1) = 4

3. xy′′′ – y′′ + 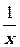= 1

4. y”+y=2cos4x+3cos4x

Вариант 15

1. Вычислить неопределенный интеграл:

а) ; б)

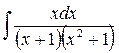
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, заданной уравнением

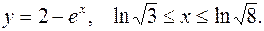
5. Вычислить длину дуги, заданной уравнением

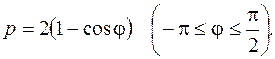
6. Решить дифференциальные уравнения

1. y′ =

2. y′ + = x³, y(1) = -5/6

3. x y′′′ + y′′ + x = 0

4. y”-4y’+8y== e^x(-sinx+2cosx)

Вариант 16

1. Вычислить неопределенный интеграл:

а) 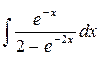; б)

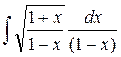
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, заданной уравнением

5. Вычислить длину дуги, заданной системой уравнений

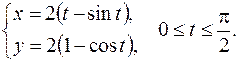
6. Решить дифференциальные уравнения

1. y′ =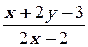

2. y′ + = 3x, y(1) = 1

3. 4y³ y′′ = y⁴ – 1, y(0) = 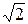, y′ (0) =

4. y”-4y’+4y== e^2xsin6x

Вариант 17

1. Вычислить неопределенный интеграл:

а) ; б)

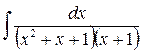
2. Вычислить определенные интегралы:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги кривой

5. Вычислить длину дуги кривой

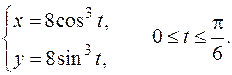
6. Решить дифференциальные уравнения

1. y′ =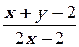

2. y′ – = 1 + x², y(1) = 3

3. y′′ = 128y³, y(0) = 1, y′ (0) = 8

4. y”-4y’+4y== -e^2xsin6x

Вариант 18

1. Вычислить неопределенный интеграл:

а) ; б)

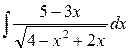
2. Вычислить определенные интегралы:

а) ; б)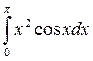

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги кривой

5. Вычислить длину дуги кривой

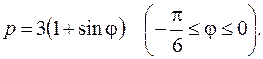
6. Решить дифференциальные уравнения

1. y′ =

2. y′ + y = 1, y(1) = 1

3. y′′ y³ + 64 = 0, y(0) = 4, y′ (0) = 2

4. y”+y=2cos7x+3sin7x

Вариант 19

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенные интегралы:

а) 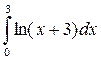; б)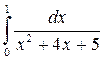

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги кривой

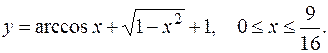
5. Вычислить длину дуги кривой

6. Решить дифференциальные уравнения

1. y′ =

2. y′ + = , y(1) = 1

3. y′′ + 2 sin y cos³ y, y(0) = 0, y′ (0) = 1

4. y”-4y’+8y= e^x(5sinx-3cosx)

Вариант 20

1. Вычислить неопределенный интеграл:

а) ; б)

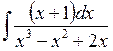
2. Вычислить определенные интегралы:

а) ; б)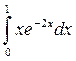

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги кривой

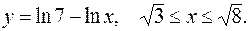
5. Вычислить длину дуги кривой

6. Решить дифференциальные уравнения

1. y′ =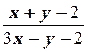

2. y′ + 2xy = -2x³, y(1) = e^-1

3. y′′ = 32 sin³ y cos y, y(1) = π/2, y′ (1) = 4

4. y”-4y’+4y= e^2xsin3x

Вариант 21

1. Вычислить неопределенный интеграл:

а) ; б)

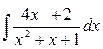
2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Найти длину дуги кривой, заданной уравнением

5. Найти длину дуги кривой, заданной уравнением

6. Решить дифференциальные уравнения

1. y′ =

2. y′ – 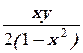= , y(0) = 2/3

3. y′′ = 98y³, y(1) = 1, y′ (1) = 7

4. y”+y=2cos3x-3sin3x

Вариант 22

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

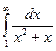
4. Найти длину дуги кривой, заданной уравнением

5. Найти длину дуги кривой, заданной уравнением

6. Решить дифференциальные уравнения

1. y′ =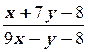

2. y′ + xy = -x³, y(0) = 3

3. y′′ y³ + 49 = 0, y(3) = -7, y′ (3) = -1

4. y”-4y’+8y=e^x(-3sinx+4cosx)

Вариант 23

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) 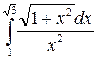; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Найти длину дуги кривой, заданной уравнением

5. Найти длину дуги кривой

6. Решить дифференциальные уравнения

1. y′ =

2. y′ – 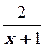y = e^x (x + 1)², y(0) = 1

3. 4y³ y′′ = 16y⁴ – 1, y(0) = , y′ (0) =

4. y”-4y’+4y=e^2xsin5x

Вариант 24

1. Вычислить неопределенный интеграл:

а) 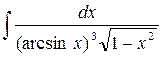; б)

2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

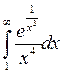
4. Найти длину дуги кривой

5. Найти длину дуги кривой

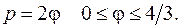
6. Решить дифференциальные уравнения

1. y′ =

2. y′ + 2xy = x sin x, y(0) = 1

3. y′′ + 8sin y cos³ y = 0, y(0) = 0, y′ (0) = 2

4. y”+2y’+5y=-17sin2x

Вариант 25

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) ; б)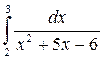

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги кривой, заданной уравнением

5. Найти длину дуги кривой

6.

5. Решить дифференциальные уравнения

1. y′ =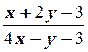

2. y′ – 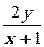= (x + 1)³, y(0) = ½

3. y′′ = 72y³, y(2) = 1, y′ (2) = 6

4. y”-4y’+8y=e^x(3sinx+5cosx)

Вариант 26

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) 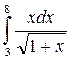; б)

3. Найти несобственный интеграл или доказать его расходимость:

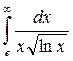
4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнениями:

.

6. Решить дифференциальные уравнения

1. y′ =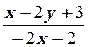

2. y′ – y cos x = -sin 2x, y(0) = 3

3. y′′ y³ + 36 = 0, y(0) = 3, y′ (0) = 2

4. y”-4y’+4y=-e^2xsin4x

Вариант 27

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) 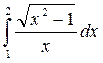; б)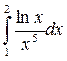

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

6. Решить дифференциальные уравнения

1. y′ =

2. y′ – 4xy = -4x³, y(0) = - ½

3. y′′ = 18 sin³ y cos y, y(1) = π/2, y′ (1) = 3

4. y”+y=2cos7x-3sin7x

Вариант 28

1. Вычислить неопределенный интеграл:

а) ; б)

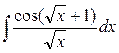
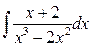
2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

6. Решить дифференциальные уравнения

1. y′ =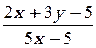

2. y′ – = - , y(1) = 1

3. 4y³y′′ = y⁴ – 64 = 0, y(0) = 2 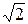, y′ (0) = 1/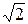

4. y”-4y’+8y=e^x(2sinx-cosx)

Вариант 29

1. Вычислить неопределенный интеграл:

а) 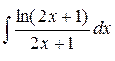; б)

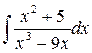
2. Вычислить определенный интеграл:

а) ; б)

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

5. Вычислить длину дуги, ограниченной линией, заданной уравнением:

.

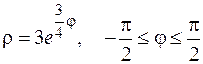6. Решить дифференциальные уравнения

1. y′ =

2. y′ – 3x² y = x² (1 + x³)/3, y(0) = 0

3. y′′ = 50y³, y(3) = 1, y′ (3) = 5

4. y”-4y’+4y=e^2xsin4x

Вариант 30

1. Вычислить неопределенный интеграл:

а) ; б)

2. Вычислить определенный интеграл:

а) 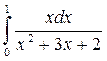; б)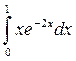

3. Найти несобственный интеграл или доказать его расходимость:

4. Вычислить длину дуги, ограниченной линией, заданной уравнением:

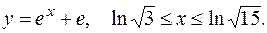
5. Вычислить длину дуги, ограниченной линией, заданной уравнением:

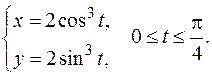
6. Решить дифференциальные уравнения

1. y′ =

2. y′ – y cos x = sin 2x, y(0) = -1

3. y′′ y³ + 25 = 0, y(2) = -5, y′ (2) = -2

4. y”+2y’+5y=10cosx

Критерии оценки:

- оценка «зачтено» выставляется студенту, если выполнено правильно более 60 процентов работы;

-оценка «не зачтено» выставляется студенту, если выполнено правильно менее 60 процентов работы.

Комплект заданий для контрольной работы№ 2

по дисциплине __ Математика_(2 семестр)_________________

5. ^{(наименование дисциплины)}

Тема: Интегральное исчисление функций нескольких переменных

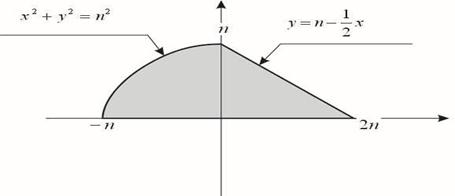
1. Представить двойной интеграл 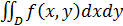в виде суммы двукратных интегралов: а) внешний интеграл по y; б) внешний интеграл по x.

1 – 5 варианты:

1. n=1

2. n=2

3. n=3

4. n=4

5. n=5

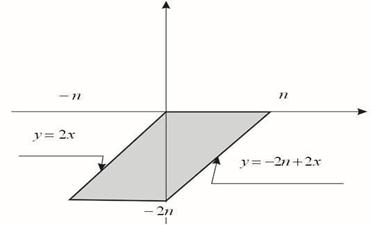
6 – 10 варианты:

6. n=1

7. n=2

8. n=3

9. n=4

10. n=5

11 – 15 варианты:

11. n=1

12. n=2

13. n=3

14. n=4

15. n=5

16 – 20 варианты:

16. n=1

17. n=2

18. n=3

19. n=4

20. n=5

21 – 25 варианты:

21. n=1

22. n=2

23. n=3

24. n=4

25. n=5

26 – 30 варианты:

26. n=1

27. n=2

28. n=3

29. n=4

30. n=5

2. Вычислить двойной интеграл в случаях:

а) прямоугольной области, заданной неравенствами;

б) произвольной области, ограниченной линиями.

1. f(x, y)=xy

а) D: 0≤x≤1, -1≤y≤0;

б) D: , , x=1, x=0.

2. f(x, y)=xy

а) D: 0≤x≤2, -1≤y≤1;

б) D: , , 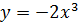x=1, x=0.

3. f(x, y)=xy

а) D: 0≤x≤3, -1≤y≤2;

б) D: , , x=1, x=0.

4. f(x, y)=xy

а) D: 0≤x≤4, -1≤y≤3;

б) D: , , x=1, x=0.

5. f(x, y)=xy

а) D: 0≤x≤5, -1≤y≤4;

б) D: , , x=1, x=0.

6. f(x, y)=x+2y

а) D: -1≤x≤0, 0≤y≤2;

б) , , x=0, x=1.

7. f(x, y)=x+2y

а) D: -2≤x≤0, 0≤y≤3;

б) , , x=1, x=2.

8. f(x, y)=x+2y

а) D: -3≤x≤0, 0≤y≤4;

б) , , x=2, x=3.

9. f(x, y)=x+2y

а) D: -4≤x≤0, 0≤y≤5;

б) , , x=3, x=4.

10. f(x, y)=x+2y

а) D: -5≤x≤0, 0≤y≤6;

б) , , x=5, x=6.

11. f(x, y)=x²y+y

а) D: , -2≤y≤2;

б) , , y=1, y=4.

12. f(x, y)=x²y+y

а) D: 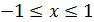, -2≤y≤3;

б) , , y=2, y=5.

13. f(x, y)=x²y+y

а) D: 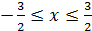, -2≤y≤4;

б) , , y=3, y=6.

14. f(x, y)=x²y+y

а) D: 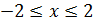, -2≤y≤5;

б) , , y=4, y=7.

15. f(x, y)=x²y+y

а) D: 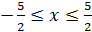, -2≤y≤6;

б) , , y=5, y=8.

16. f(x, y)=(x+y)²

а) D: 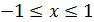, 0≤y≤3;

б) 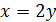, x 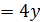, x=1.

17. f(x, y)=(x+y⁾²

а) D: , 0≤y≤4;

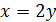б) , x 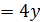, x=2.

18. f(x, y)=(x+y)²

а) D: , 0≤y≤5;

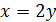б) , x 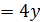, x=3.

19. f(x, y)=(x+y)²

а) D: 2 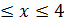, 0≤y≤6;

б) 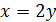, x 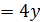, x=4.

20. f(x, y)=(x+y)²

а) D: 3 , 0≤y≤7;

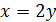б) , x 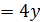, x=5.

21. f(x, y)=x²+3y

а) D: 0 , -1≤y≤0;

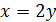б) , x 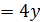, y=2, y=3.

22. f(x, y)=x²+3y

а) D: 0 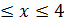, -2≤y≤0;

б) 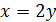, x 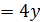, y=3, y=4.

23. f(x, y)=x²+3y

а) D: 0 , -3≤y≤0;

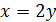б) , x 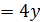, y=4, y=5.

24. f(x, y)=x²+3y

а) D: 0 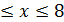, -4≤y≤0;

б) 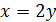, x 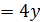, y=5, y=6.

25. f(x, y)=x²+3y

а) D: 0 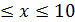, -5≤y≤0;

б) 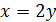, x 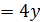, y=6, y=7.

26. f(x, y)=5x – y

а) D: -1 , -1≤y≤3;

б) 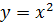, , x=1, x=2.

27. f(x, y)=5x – y

а) D: -2 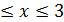, -2≤y≤3;

б) 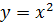, , x=1, x=3.

28. f(x, y)=5x – y

а) D: -3 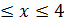, -3≤y≤3;

б) 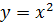, , x=1, x=4.

29. f(x, y)=5x – y

а) D: -1 , -4≤y≤3;

б) 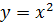, , x=1, x=5.

3. Вычислить тройной интеграл по прямоугольной области.

1. , D: 0≤x≤1, 1≤y≤2, 0≤z≤3.

2. , D: 0≤x≤2, 1≤y≤4, 0≤z≤3.

3. , D: 0≤x≤3, 1≤y≤6, 0≤z≤3.

4. , D: 0≤x≤4, 1≤y≤8, 0≤z≤3.

5. , D: 0≤x≤5, 1≤y≤10, 0≤z≤3.

6. , D: -1≤x≤0, 0≤y≤1, 1≤z≤2.

7. , D: 0≤x≤1, 1≤y≤2, 0≤z≤3.

8. , D: 0≤x≤1, 1≤y≤2, 0≤z≤3.

9. , D: 0≤x≤1, 1≤y≤2, 0≤z≤3.

10. , D: 0≤x≤1, 1≤y≤2, 0≤z≤3.

11. , D: -1≤x≤0, 0≤y≤2, 0≤z≤1.

12. , D: -2≤x≤0, 0≤y≤2, 0≤z≤2.

13. , D: -3≤x≤0, 0≤y≤2, 0≤z≤3.

14. , D: -4≤x≤0, 0≤y≤2, 0≤z≤4.

15. , D: -5≤x≤0, 0≤y≤2, 0≤z≤5.

16. , D: 0≤x≤2, -2≤y≤1, -1≤z≤1.

17. , D: 0≤x≤4, -2≤y≤2, -1≤z≤1.

18. , D: 0≤x≤6, -2≤y≤3, -1≤z≤1.

19. , D: 0≤x≤8, -2≤y≤4, -1≤z≤1.

20. , D: 0≤x≤10, -2≤y≤5, -1≤z≤1.

4. Найти объем и массу тела Ω, если μ – его плотность.

1. Ω: ; , x≥0, μ=x.

2. Ω: ; , x≥0, μ=x.

3. Ω: 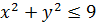; , x≥0, μ=x.

4. Ω: 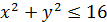; , x≥0, μ=x.

5. Ω: ; , x≥0, μ=x.

6. Ω: 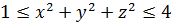; z≥0, y≥0, μ=2z.

Поиск по сайту: