Аналитическое описание движения

3.

Уравнение движения для электрона в декартовых координатах (рис.12.2) таковы:

(12.2)

где

(12.3)

Удобнее, однако, рассматривать движение электрона в цилиндрических координатах, где независимыми переменными будут радиус-вектор и угол поворота электрона (см.рис.12.2). Для этого используются известные соотношения между координатами:

(12.4)

После подстановки (1.4) в (1.2) и некоторых преобразований, уравнение движения принимает вид

(12.5)

где

Интегрирование этого уравнения с учетом начальных условий движения электрона приводит к соотношению

(12.6)

где 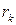— радиус катода.

Так как напряженность электрического поля вблизи поверхности катода наибольшая, то можно считать, что уже у поверхности катода электрон приобретает максимальную скорость и поэтому в остальной части межэлектродного пространства он движется с почти постоянной скоростью. Как показывает анализ, в таком случае большая часть траектории электрона будет близка к окружности, и движение по ней будет происходить с угловой скоростью . Период вращения электрона по такой траектории определяется известным соотношением:

(12.7)

и зависит только от величины магнитного поля .

Еще раз повторим, что в случае многоэлектронного приближения, вследствие разброса начальных скоростей электронов, а также некоторой неэквипотенциальности поверхности катода вдоль его длины и возможной асимметрии расположения электродов лампы, «отсечка» тока в лампе при происходит в некотором интервале значений (рис.12.4).

Рассмотрим движение электрона по критической траектории . В этом случае радиальная составляющая 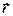скорости электрона в точке поворота при равна нулю. Однако тангенциальная (линейная) составляющая скорости электрона отлична от нуля и приближенно равна

(12.8)

где — угловая скорость вращательного движения электрона (по окружности).

Так как электрон движется в потенциальном электрическом поле, а сила Лоренца не совершает работы, то полная энергия электрона постоянна. Для критической траектории имеем:

(12.9)

откуда

(12.10)

Подставляя в (12.10) выражение для из соотношения (12.6), получим:

(12.11)

Это и есть основное выражение для экспериментального определения величины .

Величина индукции магнитного поля соленоида, учитывая, что его длина соизмерима с диаметром , вычисляется по формуле (см. лаб.работу № 10):

(12.12)

где = 4 10^-7 Гн/м, - ток в цепи соленоида, соответствующий критической ситуации, N — число витков.

Таким образом, по экспериментальному значению можно вычислить по формуле (12.11) величину .

Поиск по сайту: