Преобразования Лоренца и «парадоксы» релятивистской кинематики

Восстановив в правах принцип относительности и по­стулировав постоянство скорости света во всех ИСО, Эйн­штейн показал, что несоответствие уравнений Максвел­ла принципу относительности связано с «некорректно­стью» применения преобразований Галилея и что на самом деле переход от координат и времени одной ИСО к координатам и времени другой ИСО необходимо про­изводить, используя другие формулы. Эти формулы на­зываются преобразованиями Лоренца. Для частного слу­чая, когда Т'-система отсчета перемещается с постоян­ной скоростью Vвдоль оси х T-системы отсчета, они имеют следующий вид:

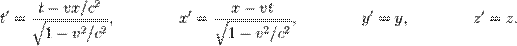
где с — скорость света в вакууме.

Уравнения Максвелла оказываются инвариантными относительно преобразований Лоренца, что полностью устраняет все противоречия классической электродина­мики с принципом относительности. В то же время легко увидеть, что старые преобразования Галилея являются частным случаем преобразований Лоренца, соответствую­щим движению объектов с малыми (по сравнению со скоростью света) скоростями. Следствием преобразований Лоренца является несколь­ко выводов, которые на первый взгляд носят «парадоксаль­ный» характер, но которые, тем не менее, совершенно ре­альны и неоднократно выдерживали опытную проверку.

1. «Сокращение» длины движущихся объектов.

Представим себе неподвижную линейку длиной L_o. Эта длина называется собственной длиной линейки, а система отсчета, в которой линейка неподвижна, — собственной системой отсчета, которую мы в дальнейшем будем обо­значать Т_о. Если линейка движется со скоростью Vотно­сительно другой системы отсчета Т, то для наблюдателя в этой системе отсчета линейка будет казаться короче, так что ее длина Lможет быть вычислена по формуле:

Следует отметить, что такое «сокращение» длины не связано с какими-то деформациями самой линейки, оно обусловлено тем, что одновременная фиксация концов движущейся линейки наблюдателем, находящимся в Т-системе отсчета, является неодновременной в другой, в частности, в собственной системе отсчета. В результа­те, например, из Т₀-системы отсчета кажется, что снача­ла фиксируется положение правого конца линейки, а че­рез некоторое время, когда линейка сместится на неко­торое расстояние, фиксируется положение левого конца. Поэтому расстояние между этими засечками оказывает­ся меньше, чем L_o. Но, увы, наблюдатель в Т-системе от­счета справедливо считает, что он фиксирует концы ли­нейки одновременно, и заставить его измерять длину иначе нельзя. Этим и объясняется парадокс «сокраще­ния длины. Обратим внимание также на то, что попе­речные размеры движущихся тел не изменяются по срав­нению с неподвижными.

Но ведь то, что касается концов линейки, в полной мере относится и к любым точкам пространства, даже если ни­каких линеек в нем нет. Поэтому можно сказать, что про­странство имеет разную метрику в разных ИСО.

Важнейшим следствием рассмотренного «парадокса» является относительный характер электрического и маг­нитного полей: электрическое поле, в одной ИСО может стать магнитным полем в другой ИСО и наоборот. Таким образом, релятивистские эффекты проявляются не толь­ко при движении с околосветовыми скоростями, они оп­ределяют и некоторые хорошо знакомые явления нашей повседневной жизни.

2. «Замедление» хода движущихся часов.

Назовем событием любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x,y,z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т. п. Рассмотрим интервал времени τ между двумя со­бытиями в Т-системе отсчета и интервал времени τ₀ между теми же событиями в Т₀-системе отсчета.

Можно доказать, что эти интервалы связаны друг с другом следующим соотношением:

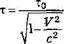
Таким образом, время в движущейся сис­теме отсчета течет медленнее, чем в неподвижной.

Здесь надо отметить, что указанное замедление отно­сится не только к часам специального вида, но и ко всем движущимся объектам. В частности, даже процессы ста­рения живых организмов замедляются, если эти организ­мы движутся. Из двух близнецов тот, который отправля­ется в космическое путешествие (назовем его Иван), ста­реет медленнее, чем его брат (Михаил), остающийся на Земле. С этим примером связан знаменитый «парадокс близнецов», который заключается в следующем. Если Иван через какое-то время вернется на Землю, то он дол­жен увидеть своего брата Михаила заметно постаревшим (предполагается, конечно, что Иван перемещался с око­лосветовой скоростью). Это следует из того, что Иван дви­гался, а Михаил оставался неподвижным («с точки зре­ния» Михаила). Но ведь можно встать на «точку зрения» Ивана, который считает себя неподвижным и относитель­но которого его брат Михаил сначала удалялся, а потом вернулся. И тогда следует считать, что Иван постареет больше, чем Михаил.

Таким образом, мы приходим к двум взаимоисключаю­щим друг друга выводам. Разрешение «парадокса близне­цов» связано с тем, что его участники, близнецы Иван и Михаил, находились в несимметричных условиях. Чтобы вернуться на Землю, Иван должен был изменить свою ско­рость на противоположную, то есть какое-то время нахо­диться в неинерциальной системе отсчета, для которой выводы СТО неприменимы. В то же время Михаил все вре­мя находился в ИСО. С учетом этого, именно Иван ока­жется моложе, чем Михаил.

3. Релятивистский закон преобразованияскоростей.

Xорошо известна форму­ла преобразования скоростей при переходе из одной (Т)ИСО в другую (Т');

u = u' + ʋ, (1.1)

где ʋ — скорость T'-системы отсчета относительно T-сис­темы отсчета. Чтобы получить эту формулу, достаточно продифференцировать по времени соотношение:

r'( t' )=r(t)- ʋt (1.2)

В релятивистской кинематике указанная формула не имеет места, а преобразования скоростей производятся по более сложным формулам, согласованным с преобразова­ниями Лоренца. Непосредственным следствием преобразований Лоренца является релятивистское правило сложения скоростей. Если некоторый объект имеет компоненты скорости относительно системы Т и — относительно Т', то между ними существует следующая связь:

В этих соотношениях относительная скорость движения систем отсчёта ʋ направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях () переходит в классический закон сложения скоростей. Если объект движется со скоростью света вдоль оси x относительно системы Т, то такая же скорость у него будет и относительно Т': . Это означает, что скорость является инвариантной (одинаковой) во всех ИСО.

Поиск по сайту: