АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Исследователь вносит гипотезу о структуре ящика

Читайте также:
  1. II Место дисциплины в структуре ООП ВПО
  2. Анализ изменений в составе и структуре активов баланса предприятия
  3. Большая доля амортизации в структуре себестоимости соответствует ________________ производству.
  4. В структуре личности он выделил три сферы: бессознательную, предсознательную и сознательную.
  5. В структуре национальной безопасности
  6. В структуре современной экономической науки
  7. Взаимосвязь личности и субъекта в целостной структуре индивидуальности.
  8. Влияние на развитие человека понятий о структуре и роли семьи
  9. Воздушный транспорт в транспортной инфраструктуре мира
  10. Глава 1 СУЩНОСТЬ ВОСПИТАНИЯ И ЕГО МЕСТО В ЦЕЛОСТНОЙ СТРУКТУРЕ ПРОЦЕССА ФОРМИРОВАНИЯ ЧЕЛОВЕКА
  11. ГЛАВА 4 ОБЪЕМНО-СИЛОВОЙ ТРЕНИНГ ПО СТРУКТУРЕ ВВОДНОГО ТРЕНИНГА
  12. Глава 6. ОБЩИЕ СВЕДЕНИЯ О ТЕХНОЛОГИЧЕСКОЙ СТРУКТУРЕ ХОЗЯЙСТВЕННОГО КОМПЛЕКСА РЕСПУБЛИКИ БЕЛАРУСЬ ... 89

Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, то есть гипотеза имеет вид: Y = A 1 X + A 0 (рис. 2.2).

2) Определение неизвестных коэффициентов A 0 и A 1 модели

Линейная одномерная модель (рис. 2.3).

 
Рис. 2.3. Одномерная модель черного ящика

Для каждой из n снятых экспериментально точек вычислим ошибку (Ei) между экспериментальным значением (Yi Эксп.) и теоретическим значением (Yi Теор.), лежащим на гипотетической прямой A 1 X + A 0 (см. рис. 2.2):

Ei = (Yi Эксп. – Yi Теор.), i = 1, …, n;

Ei = Yi – A 0 – A 1 · Xi, i = 1, …, n.

Ошибки Ei для всех n точек следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F уже одного знака:

Ei 2 = (Yi – A 0 – A 1 · Xi)2, i = 1, …, n.

Цель метода — минимизация суммарной ошибки F за счет подбора коэффициентов A 0, A 1. Другими словами, это означает, что необходимо найти такие коэффициенты A 0, A 1 линейной функции Y = A 1 X + A 0, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов.

Суммарная ошибка F является функцией двух переменных A 0 и A 1, то есть F (A 0, A 1), меняя которые, можно влиять на величину суммарной ошибки (см. рис. 2.4).

 
Рис. 2.4. Примерный вид функции ошибки

Чтобы суммарную ошибку минимизировать, найдем частные производные от функции F по каждой переменной и приравняем их к нулю (условие экстремума):

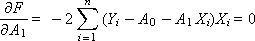
После раскрытия скобок получим систему из двух линейных уравнений:

Для нахождения коэффициентов A 0 и A 1 методом Крамера представим систему в матричной форме:

Решение имеет вид:

Вычисляем значения A 0 и A 1.


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)