Закон Малюса. Ни двойное лучепреломление, ни закон Малюса не нашли объяснения в рамках теории продольных волн

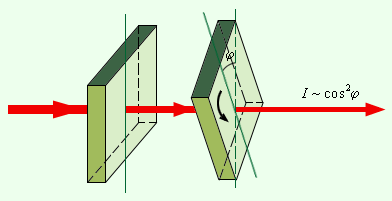
Ни двойное лучепреломление, ни закон Малюса не нашли объяснения в рамках теории продольных волн.

Для продольных волн направление распространения луча является осью симметрии. В продольной волне все направления в плоскости, перпендикулярной лучу, равноправны.

В поперечной волне (например, в волне, бегущей по резиновому жгуту) направление колебаний и перпендикулярное ему направление неравноправны. Таким образом, асимметрия относительно луча является решающим признаком, который отличает поперечную волну от продольной.

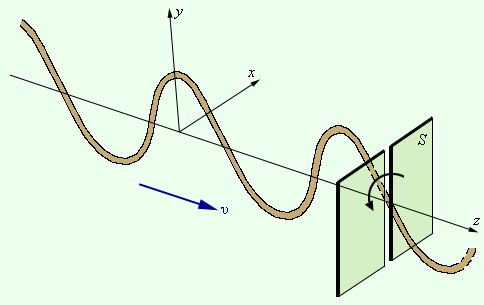
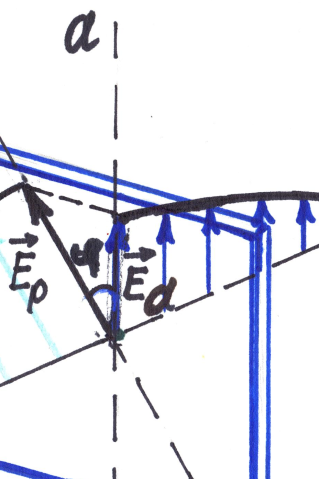
С помощью разложения вектора на составляющие по осям можно объяснить закон Малюса.

Любую волну (поляризованную и неполяризованную) можно представить как суперпозицию двух линейно-поляризованных во взаимно перпендикулярных направлениях волн:

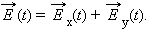
Но в поляризованной волне обе составляющие E_x(t) и E_y(t) когерентны, а в неполяризованной – некогерентны, т. е. в первом случае разность фаз между E_x(t) и E_y(t) постоянна, а во втором она является случайной функцией времени.

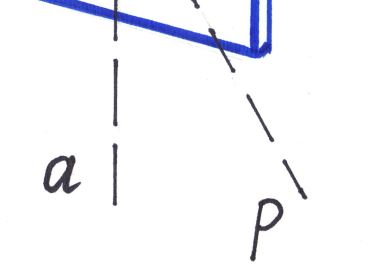
Рассмотрим прохождение естественного света последовательно через два идеальных поляроида П₁ и П₂ (рис.), разрешенные направления которых развернуты на некоторый угол φ.

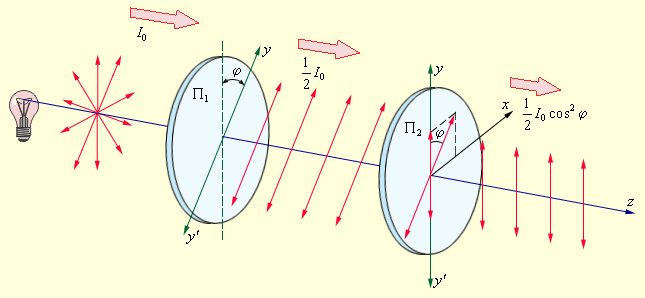
У многих кристаллов поглощение света сильно зависит от направления электрического вектора в световой волне. Это явление называют дихроизмом.

Этим свойством, в частности, обладают пластины турмалина, использованные в опытах Малюса. При определенной толщине пластинка турмалина почти полностью поглощает одну из взаимно перпендикулярно поляризованных волн (например, E_x) и частично пропускает вторую волну (E_y). Направление колебаний электрического вектора в прошедшей волне называется разрешенным направлением пластинки. Пластинка турмалина может быть использована как для получения поляризованного света, так и для анализа характера поляризации света (поляризатор Р и анализатор А).

E_x = E _o cosφ, E_y = E _o sin φ,

E_x – пройдет через поляризатор, а E_y – не пройдет.

Т.к. J ~ E ², то J ~ E_о² cos² φ и J _о ~ E_о²

закон Малюса: J = J _о сos² φ

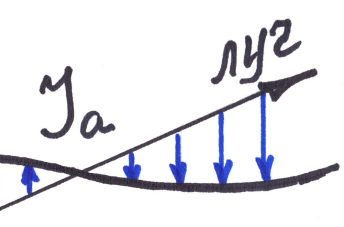
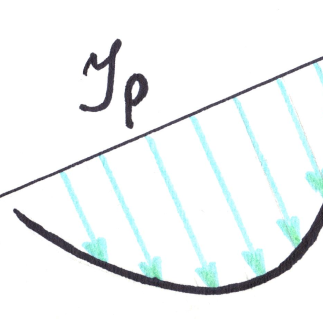
В естественном свете все значения φ равновероятны и среднее значение < cos² φ >=1/ 2. Поэтому интенсивность естественного света, прошедшего один поляризатор уменьшается в два раза.

Поставим на пути естественного света два поляризатора, плоскости которых образуют угол φ.

Из первого поляризатора выйдет луч интенсивностью

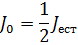
Согласно закону Малюса интенсивность света, прошедшего второй поляризатор,

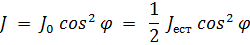
Это без учета поглощения света в кристалле.

J = J_max = 1/2 J_ест при φ = 0.

При φ = π/2 J = 0 – скрещенные поляризаторы свет не пропускают. Таким образом, в электромагнитной теории света закон Малюса находит естественное объяснение на основе разложения вектора на составляющие.

Поиск по сайту: