Получение эллиптически поляризованного света

Прохождение света через анизотропное вещество, оптические свойства которого в разных направлениях не одинаковы, сопровождается рядом явлений, имеющих большое практическое значение для исследования закономерностей распространения света в изотропной среде. Так, в предлагаемой лабораторной работе для получения в изотропной среде света эллиптической поляризации используется явление двойного лучепреломления в кристаллической пластинке ниобата лития ().

При падении световой волны на границу анизотропной среды (в частности, на кристалл ) в этой среде возникают две волны, распространяющиеся от границы в разных направлениях и с разными скоростями. Это явление называется двойным лучепреломлением. Установлено, что выходящие из кристалла световые волны линейно поляризованы во взаимно перпендикулярных направлениях (рис.13).

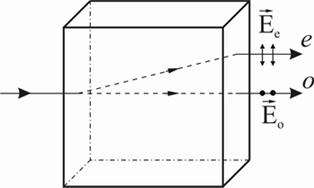
Рис. 13. Двойное лучепреломление в кристалле.

(На рисунке - колебания вектора , перпендикулярные плоскости чертежа, обозначены точками, а колебания, параллельные плоскости чертежа, изображены двусторонними стрелками)

В одноосных кристаллах (например, в ) имеется одно направление, в котором не наблюдается двойного лучепреломления. Это направление называется оптической осью кристалла. Волна, в которой вектор совершает колебания перпендикулярно оптической оси кристалла, называется обыкновенной (o); ее скорость по различным направлениям в кристалле одинакова. Вторая волна, у которой направления колебаний вектора составляют разные углы с оптической осью (в зависимости от угла падения), называется необыкновенной (e). Скорость необыкновенной волны в кристалле зависит от направления; в разных кристаллических средах она может быть больше или меньше скорости обыкновенной волны. В направлении оптической оси скорости обыкновенной и необыкновенной волн равны.

Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси. При нормальном падении на такую пластинку линейно поляризованного света обыкновенная и необыкновенная волны оказываются когерентными. На входе в пластинку разность фаз этих волн равна нулю. Разность их фаз на выходе из пластинки возникает за счет различия в скорости распространения ортогонально поляризованных волн (o и e) в кристалле и определяется формулой:

, (6)

где d - толщина пластинки; - показатель преломления для волны, в которой вектор перпендикулярен оптической оси; - для волны, в которой вектор параллелен оптической оси; - длина волны в вакууме.

Вырезанная параллельно оптической оси пластинка, для которой

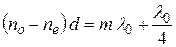(7)

(), называется пластинкой в четверть волны (пластинка «»). При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз, равную .

Следовательно, если на пластинку «» направить перпендикулярно линейно поляризованный свет, в котором в общем случае направление колебания составляет некоторый угол с оптической осью кристалла (ОО), то из пластинки выйдет эллиптически поляризованный свет, причем главные оси эллипса будут направлены вдоль оптической оси кристалла и перпендикулярно ей (рис.14).

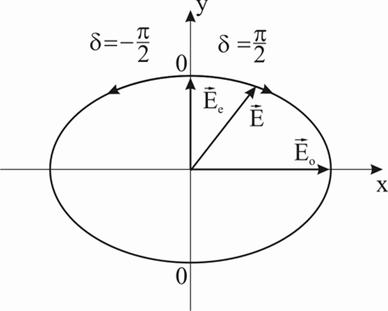
Рис. 14. Эллипс поляризации для случая ,

В частном случае, если угол между оптической осью кристалла и направлением колебания падающей линейно поляризованной волны составляет 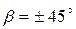(так как только в этом случае равны амплитуды волн, между которыми пластинка «» вносит сдвиг фаз ), то эллипс обращается в круг, т.е. имеет место круговая или циркулярная поляризация (рис.15).

Рис. 15. Получение света круговой поляризации

Поиск по сайту: