Поляризация плоских монохроматических световых волн

В плоской электромагнитной волне векторы и взаимно перпендикулярны и тройка векторов 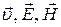составляет правовинтовую систему. В этом заключается свойство поперечности электромагнитных волн. Кроме того, векторы и в бегущей плоской монохроматической волне колеблются синфазно, т.е. они одновременно и в одних и тех же точках пространства достигают максимального и минимального значения.

На рис.2 представлен «мгновенный снимок» Рис. 2.Линейно поляризованная световая волна

плоской монохроматической световой волны, показывающий векторы и в разных точках оси z в один момент времени (на рисунке ось z совпадает с направлением распространения волны). Подобная волна, т.е. волна, для которой направления колебаний векторов и остаются неизменными, называется линейно поляризованной или (плоско поляризованной).

Плоскость, которая проходит через электрический вектор и направление распространения волны z, называется плоскостью поляризации (или плоскостью колебаний световой волны) (рис.2). Тогда линейно или плоско поляризованная световая волна – это волна, у которой плоскость поляризации не меняет своего положения в пространстве. В этом случае конец электрического вектора в любой точке пространства со временем описывает прямую линию, перпендикулярную направлению распространения волны.

В рассмотренном примере линейно поляризованной волны вектор во всех точках направлен параллельно оси x (см. рис.2). Однако в изотропном пространстве все направления в плоскости xy, перпендикулярной направлению распространения волны, эквивалентны. Поэтому вектор может иметь любое направление в этой плоскости.

В связи с этим рассмотрим электрическое поле световой волны, возникающей при сложении двух монохроматических волн с ортогональными направлениями линейной поляризации, различающихся по фазе на (рис.3):

(3)

Рис. 3.Две когерентные линейно поляризованные волны

с ортогональными направлениями колебаний

Результирующая напряженность является векторной суммой напряженносте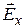й и (рис.4). Угол 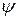между направлениями векторов 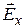и определяется выражением

. (4)

Рис. 4. Вектор как результат сложения двух взаимно перпендикулярных

векторов 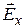и

Введем определение. Две волны называются когерентными, если разность их фаз не зависит от времени. Примем во внимание, что в силу монохроматичности световые волны и являются когерентными.

Пусть разность фаз или 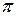, тогда

.

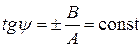Следовательно, результирующее колебание совершается в фиксированном направлении – волна оказывается линейно поляризованной.

В случае, когда и , из соотношения (4) следует, что

.

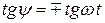Это означает, что плоскость поляризации поворачивается вокруг направления луча (линии, вдоль которой распространяется световая энергия) с угловой скоростью, равной частоте колебания 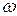, а конец электрического вектора в любой заданной точке с течением времени описывает окружность. Световая волна в этом случае называется поляризованной по кругу или циркулярно поляризованной. На рис.5 представлен «мгновенный снимок» такой волны. Из этого рисунка видно, что концы векторов для разных значений z лежат на винтовой линии. Чтобы с помощью рис.5 представить поведение вектора с течением времени, можно считать, что весь этот «винт», оставаясь на месте, вращается как целое вокруг оси z с угловой скоростью 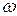либо, что он перемещается поступательно (без вращения) вдоль оси z со скоростью с.

Необходимо помнить, что все сказанное о поведении вектора в волне круговой поляризации относится и к вектору , так как в бегущей электромагнитной волне векторы и лежат в плоскости, перпендикулярной направлению распространения, в любой момент и в любой точке они перпендикулярны друг другу.

Рис. 5. Вектор в разных точках оси z для волны

с левой круговой поляризацией в фиксированный момент времени

Теперь выясним состояние поляризации результирующей волны для случая произвольного постоянного значения . Примем во внимание, что величины и представляют собой координаты конца результирующего вектора (рис.6). Из учения о колебаниях известно, что два взаимно перпендикулярных гармонических колебания одинаковой частоты при сложении дают в общем случае траекторию движения по эллипсу (в частности, может получиться траектория движения по прямой или по окружности). Аналогично конец вектора (с координатами { , }, определяемыми выражениями (3)) в любой заданной точке с течением времени описывает эллипс.

Рис. 6.Суперпозиция линейно поляризованных плоских волн,

приводящая к эллиптически поляризованной волне

Следовательно, две монохроматические линейно поляризованные световые волны, плоскости колебаний которых взаимно перпендикулярны, при наложении друг на друга дают эллиптически поляризованную световую волну. Таким образом, эллиптическая поляризация - это наиболее общий вид поляризации монохроматической волны, переходящий при определенных условиях в линейную или круговую поляризации. При разности фаз или 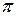эллипс вырождается в прямую и получается линейно поляризованный свет. При и равенстве амплитуд складываемых волн эллипс превращается в окружность – получается свет, поляризованный по кругу.

В зависимости от направления вращения вектора различают правую и левую эллиптическую и круговую поляризации. Если по отношению к направлению, противоположному направлению луча, вектор вращается по часовой стрелке, поляризация условно называется правой, в противном случае – левой.

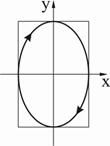
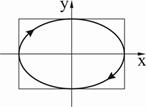
Картины поляризации результирующей волны при одинаковых амплитудах и разных фазах складываемых ортогонально поляризованных волн показаны на рис.7. Аналогичные картины, полученные при сложении волн различной амплитуды, представлены на рис.8.

Волну с произвольной (в общем случае эллиптической) поляризацией всегда можно разложить либо на сумму двух линейно поляризованных волн с ортогональными направлениями поляризации, либо на сумму двух поляризованных по кругу волн с правой и левой поляризациями.

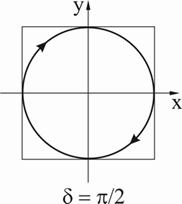
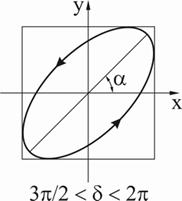
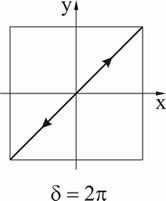
Рис. 7. Изменение состояния поляризации результирующей волны

при изменении разности фаз между исходными

ортогонально линейно поляризованными волнами одинаковой амплитуды

Рис. 8. Изменение состояния поляризации результирующей волны

при изменении разности фаз между исходными

ортогонально линейно поляризованными волнами различной амплитуды

Основными параметрами эллиптически поляризованного света являются:

1) ориентация эллипса в системе координат xoy, характеризуемая углом 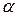, образуемым большой осью эллипса с осью x;

2) форма эллипса, характеризуемая отношением полуосей эллипса (большая 2 a и малая 2 b оси).

В свою очередь угол 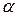и отношение зависят от разности фаз и отношения амплитуд исходных колебаний, что качественно отражено в рис. 7 и 8.

Поиск по сайту: