 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Куна-Таккера. Локальные условия Куна-Таккера
f (x 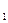 , x
, x  ,..., x
,..., x 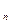 )
)
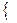 g
g 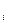 (x
(x 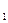 , x
, x  ,..., x
,..., x 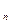 )
)  , i=
, i= 
x 
 , j=
, j= 
L(X,Y)=f(x)+ 
Можно сформулировать теорему Куна-Таккера или теорему о седловой точке.
 ,
,  - условие регулярности.
- условие регулярности.
Если функция f(x) и g 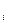 (x), i=
(x), i=  дифференцируемые функции, то можно сформулировать локальное условие Куна-Таккера:
дифференцируемые функции, то можно сформулировать локальное условие Куна-Таккера:
 | (X
| (X 
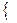 x
x 
 | (X
| (X 
x 
 | (X
| (X 
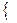

 | (X
| (X 

 , i=
, i= 
- Динамическое программирование. Метод функционального программирования. Задача распределения ресурсов.
Оптимальное решение находилось только на этапе планирования. Такие задачи часто называют одноэтапными или одношаговыми. В динамических же находится ряд оптимальных решений, обеспечивающих оптимальное развитие всего процесса в целом.
Экономический процесс называется управляемым, если можно влиять на ход его развития. Управлением называется совокупность решений, принимаемых на каждом этапе с целью влияния на ход процесса.
Пусть есть средства, которые надо вложить в развитие 2-х неоднородных предприятий. Известно, что если в 1-ое предприятие вложить y средств, а во 2-ое (x-y) средств, то доход соответственно составляет: g(y) и h(x-y)
Необходимо так выбрать величину y, чтобы общий доход W был максимальным W 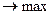 .
.
На одном этапе доход W  .Пусть g и h непрерывны, тогда максимум существует всегда.
.Пусть g и h непрерывны, тогда максимум существует всегда.
Величина W  определяет величину возможного максимального дохода в одноэтапном процессе. Просмотрим двухэтапный процесс. Предположим, что за счет издержек. необходимых для получения дохода g(y), первоначальное количество средств y уменьшилось до величины
определяет величину возможного максимального дохода в одноэтапном процессе. Просмотрим двухэтапный процесс. Предположим, что за счет издержек. необходимых для получения дохода g(y), первоначальное количество средств y уменьшилось до величины 
Аналогично, первоначальное количество средств (x-y), вложенных во вторую отрасль, уменьшилось до величины b(x-y), 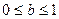 , за счет издержек, требующихся для получения дохода h(x-y). Таким образом, после осуществления одноэтапного процесса, остаток средств составляет ay+b(x-y).
, за счет издержек, требующихся для получения дохода h(x-y). Таким образом, после осуществления одноэтапного процесса, остаток средств составляет ay+b(x-y).
Повторим процесс распределения суммарного остатка, полагая, что ay+b(x-y)=x  . В результате этого распределения на втором этапе получим доход W
. В результате этого распределения на втором этапе получим доход W 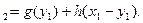
Полный доход в данном случае составляет:
W=W 
Максимальный суммарный доход получим при максимизации функции W относительно y и y  в двумерной области, опред-й этими неравенствами
в двумерной области, опред-й этими неравенствами  и
и  .
.
Рассмотрим N-этапный процесс, в котором операция распределения повторяется последовательно N-раз.
Полный доход от этого процесса W вычисляется по формуле:
W(x,y,y  .
.
x 
x 
...................................................
x  ,
,
0 
Таким образом, получили, что надо максимизировать функцию N переменных в некоторой области. Максимальное значение полного дохода зависит от N;x. Поэтому определим функцию f 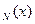 как максимальный доход, полученный от N-этапного процесса, который начинается с величины x
как максимальный доход, полученный от N-этапного процесса, который начинается с величины x  .
.
f  .
.
Тогда, исходя из условия задачи для одноэтапного процесса, получаем функциональное уравнение:
f 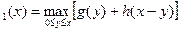
Для 2-х этапного процесса выражаем f  через f
через f  .
.
Если y 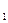 выбрана оптимально, то в результате начального распределения y от второго этапа получим доход f
выбрана оптимально, то в результате начального распределения y от второго этапа получим доход f  следующим образом:
следующим образом:
f  (g(y)+h(x-y)+f
(g(y)+h(x-y)+f 
Рассуждая, аналогично, в случае N- этапного процесса, получаем основное функциональное уравнение:
f 
При этом, на каждом этапе вычисления мы получаем не только f  но и y
но и y  так как распределение исходной величины x в начале k-го этапа было оптимальной.
так как распределение исходной величины x в начале k-го этапа было оптимальной.
Таким образом, мы привели задачу N-мерной оптимизации последовательности из N-одномерных задач.
- Теория игр. Цена игры. Седловая точка игры.
Математическая теория конфликтных ситуаций. В теории игр нас интересует стратегия, с помощью которой достигается выигрыш, максимальная возможность в данной ситуации. Основное содержание теории игр состоит в изучении следующей проблемы: если n-партнеров p 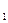 ,p
,p  ,...,p
,...,p 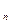 играют в данную игру G, то как должен вести партию i-ый игрок для достижения наиболее благоприятного для себя исхода. Под термином «игра»понимают совокупность предварительно оговоренных правил и условий игры, а термин «партия» связан с частной возможностью реализации этих правил.
играют в данную игру G, то как должен вести партию i-ый игрок для достижения наиболее благоприятного для себя исхода. Под термином «игра»понимают совокупность предварительно оговоренных правил и условий игры, а термин «партия» связан с частной возможностью реализации этих правил.
В дальнейшем предполагается, что в конце каждой партии игрок P 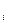 получает сумму очков V
получает сумму очков V 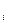 , называемую выигрышем.V
, называемую выигрышем.V 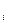 может быть:
может быть:  0,
0,  0, = 0. Если сумма всех V
0, = 0. Если сумма всех V 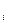 =0, то такая игра называется игрой с нулевой суммой
=0, то такая игра называется игрой с нулевой суммой  (выигрыш за счет других).
(выигрыш за счет других).
 ; * - индекс пробегает все возможные значения.
; * - индекс пробегает все возможные значения.
 - наилучшая стратегия, дающая гарантированный выигрыш.
- наилучшая стратегия, дающая гарантированный выигрыш.
 ,
,
 - нижняя цена игры.
- нижняя цена игры.
 - max-min стратегия.
- max-min стратегия.

 =
= 
 - гарантированный проигрыш.
- гарантированный проигрыш.

 - верхняя цена игры.
- верхняя цена игры.
 - min-max стратегия.
- min-max стратегия.
Если  , то это устойчивая игра. Если игроки не будут придерживаться этих чистых стратегий, то это хуже для них.
, то это устойчивая игра. Если игроки не будут придерживаться этих чистых стратегий, то это хуже для них.
Если  =
=  , то это называется чистая цена игры.
, то это называется чистая цена игры.
Игрой с полной информацией называется игра, в которой каждый игрок при каждом своем ходе знает перечень предыдущих ходов (своих и противника).
Игра с полной информацией имеет седловую точку, которой соответствует решение в чистых стратегиях A 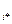 , B
, B  .
.
Такая игра всегда заканчивается с известной информацией, равной цене чистой игры.
- Теория игр. Игра в смешанных стратегиях.
Математическая теория конфликтных ситуаций. В теории игр нас интересует стратегия, с помощью которой достигается выигрыш, максимальная возможность в данной ситуации.
Основное содержание теории игр состоит в изучении следующей проблемы: если n-партнеров p 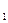 ,p
,p  ,...,p
,...,p 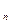 играют в данную игру G, то как должен вести партию i-ый игрок для достижения наиболее благоприятного для себя исхода. Под термином «игра»понимают совокупность предварительно оговоренных правил и условий игры, а термин «партия» связан с частной возможностью реализации этих правил. В дальнейшем предполагается, что в конце каждой партии игрок P
играют в данную игру G, то как должен вести партию i-ый игрок для достижения наиболее благоприятного для себя исхода. Под термином «игра»понимают совокупность предварительно оговоренных правил и условий игры, а термин «партия» связан с частной возможностью реализации этих правил. В дальнейшем предполагается, что в конце каждой партии игрок P 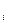 получает сумму очков V
получает сумму очков V 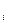 , называемую выигрышем.V
, называемую выигрышем.V 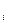 может быть:
может быть:  0,
0,  0, = 0. Если сумма всех V
0, = 0. Если сумма всех V 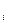 =0, то такая игра называется игрой с нулевой суммой
=0, то такая игра называется игрой с нулевой суммой  (выигрыш за счет других).
(выигрыш за счет других).
Введем понятие оптимальной смешанной стратегии.
M(X,Y)=XGY= 
X=(x 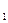 , x
, x  ,..., x
,..., x  ) - произвольные смешанные стратегии.
) - произвольные смешанные стратегии.
Y=(y 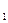 , y
, y  , …, y
, …, y 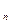 )
)
 ;
; 
0  ; 0
; 0 
Поиск по сайту: