АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные классы экстремальных задач: гладкие конечномерные и задачи классического вариационного исчисления

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. Biglnteger Классы
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.1. Пример разработки модели задачи технического контроля
  5. I. 1.2. Общая постановка задачи линейного программирования
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  11. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  12. I. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Гладкие конечномерные задачи

Пусть 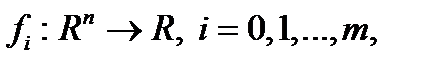— функции, n переменных, отображающие пространство Rn в R. Считаем, что все функции обладают определенной гладкостью. Гладкой конечномерной экстремальной задачей с ограничениями тира равенств и неравенств называется следующая задача в Rn :

 

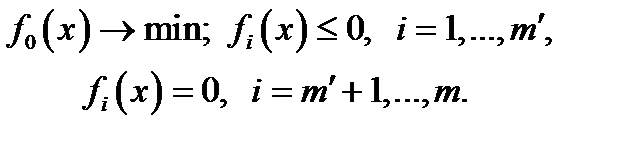
Простейшей задачей классического вариационного исчисления называется следующая экспериментальная задача в пространстве :

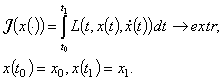
‑ называется интегрантом. Экстремум в задаче (7.1) рассматривается среди функций 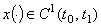, удовлетворяющих условиям на концах, или краевым условия м , такие функции называются допустимыми.

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)