АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Случай

Читайте также:
  1. Рассмотрим первый случай.
  2. Следующий случай.
  3. Теорема Куна-Таккера: общий случай.

Методические указания к лабораторным работам 1-2

ТЕМА:”ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ”

 

ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ.

МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (дихотомии).

Метод половинного деления состоит в том, что мы уменьшаем длину интервала неопределенности так, что минимум остается внутри его; процесс продолжается до тех пор, пока длина интервала неопределенности не станет меньше заданной точности. Уменьшение длины интервала производится выбором двух точек x1, x2, расположенных симметрично относительно середины отрезка и сравнением значений функции в этих точках:

Возможны три случая, приводящие к сужению длины интервала неопределенности:

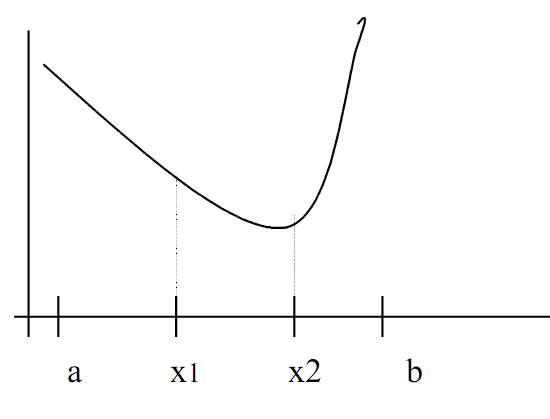
Случай.

f(x1)>f(x2)

в промежутке [a,x1] функция убывает, значит минимума нет,

поэтому новый уменьшенный интервал неопределенности [x1,b] т.е.

a:=x1.

 

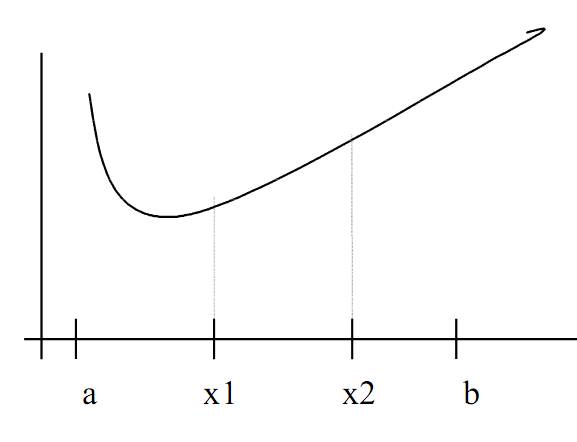
случай.

 

f(x1)<f(x2)

в промежутке [x2,b] функция возрастает, значит минимума нет,

поэтому новый уменьшенный интервал неопределенности [a,x2] т.е.

b:=x2.

 

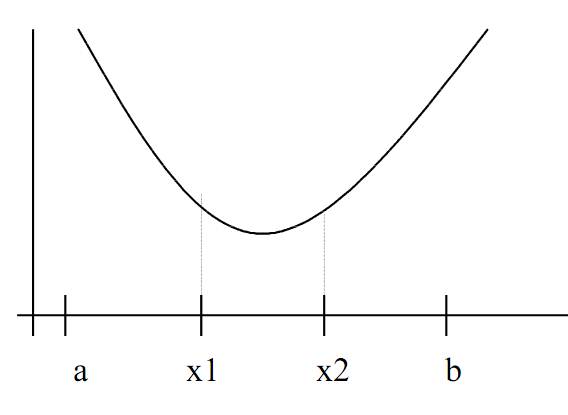
3. случай

 

f(x1)=f(x2)

минимум внутри отрезка [x1,x2], поэтому новый уменьшенный

отрезок неопределенности [x1,x2] т.е. a:=x1, b:=x2.

 

Алгоритм метода деления пополам:

1) Задать границы интервала неопределенности a, b, а также требуемую точность e;

2)

3)

 

4) ;

 

;

 

.

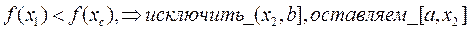2,3,4 продолжаем до тех пор, пока длина интервала неопределенности не станет меньше ε.

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)