 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Изучение дифракции Фраунгофера на одной и двух щелях и дополнительных экранах
Цель работы: освоить методы наблюдения и анализа фраунгоферовых дифракционных картин от различных препятствий.
I. Дифракция Фраунгофера на одной щели.
Пусть плоская монохроматическая волна падает нормально на узкую длинную щель. Чтобы наблюдать дифракцию Фраунгофера мы должны либо удалить экран на бесконечность (тогда в каждой точке экрана соберутся лучи, идущие параллельным пучком), либо на пути дифрагировавших лучей поставить линзу, и экран расположить в фокальной плоскости линзы. Линза будет собирать в разных точках фокальной плоскости лучи, дифрагировавшие под разными углами j и идущие параллельными пучками (рис.1).
Рис.1
Ширину щели обозначим через b. Для расчета дифракционной картины используем метод векторных диаграмм. Разобьем щель (открытую часть волновой поверхности) на узкие одинаковые зоны-полоски ширины D х, параллельные прямолинейным краям щели. Колебания, приходящие в точку Р от каждой зоны-полоски, будут иметь одинаковую амплитуду DЕ, поскольку площади зон одинаковы и лучи идут параллельным пучком. Разность хода между крайними лучами зависит от угла дифракции j и равна D = b sinj (рис.1). Соответственно, разность хода между лучами, идущими от соседних зон D¢=D x ×sinj. Так как D х =const, то разность фаз d между колебаниями, приходящими в точку Р от соседних зон-полосок, будет также одинакова: 
.
Следовательно, при графическом сложении амплитуд колебаний в точке Р, мы получим цепочку векторов D Е i, одинаковых по модулю и повернутых друг относительно друга на один и тот же угол (рис.2а).
Рис.2
Результирующая амплитуда изобразится вектором Е – хордой дуги окружности с центром в точке С. Для точки Р 0 (рис.1) эта цепочка образует прямую, что соответствует максимальной амплитуде Е 0. (рис.2б)
Если разность хода крайних лучей D=λ, то их разность фаз d=2π, цепочка оказывается замкнутой и амплитуда результирующего колебания Е = 0. (рис.2в). Это первый минимум дифракционной картины, представляющей собой симметричную относительно середины систему чередующихся светлых и темных полос, параллельных щели.
Результирующая амплитуда равна нулю и тогда, когда разность фаз d=2π m, где m = ±2, ±3… Цепочка при этом замыкается после m оборотов, практически не меняя своей длины Е 0. Таким образом, условие минимумов дифракционной картины b sinj = m λ, где m = ±1, ±2, ±3…
Найдем интенсивность света I на экране в зависимости от угла дифракции j. Результирующую амплитуду колебаний Е в точке Р легко определить из рис.2а. Если радиус дуги обозначить через R, то 
, а длина дуги Е 0 = R d, где 
. Выразив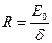 
и подставив в Е, получаем:
. (1)
Поскольку интенсивность волны I пропорциональна квадрату амплитуды, то:
. (2)
График зависимости I от sinj изображен на (рис.3).
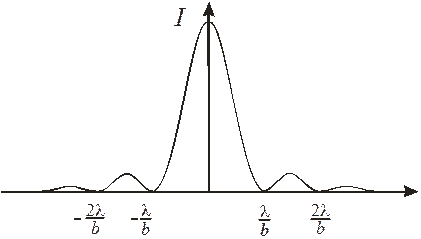
Рис.3
II. Дифракция Фраунгофера на двух щелях.
Возьмем 2 узкие щели шириной b, разделенные непрозрачным промежутком а, и направим на них нормально параллельный пучок света (рис.4). Введем величину d = a + b.
Рис.4
Если поочередно закрывать одну из щелей, то на экране будет наблюдаться одна и та же дифракционная картина (рис.3), местоположение которой определяется положением линзы, а не щели.
Если открыть обе щели одновременно, то получающаяся картина будет зависеть от когерентности излучения, идущего от соседних щелей. В отсутствие когерентности дифракционные картины от каждой щели наложились бы друг на друга и интенсивность увеличилась бы в 2 раза. При освещении щелей когерентным светом, волны от соседних щелей интерферируют друг с другом и дифракционная картина резко меняется.
В направлениях, в которых каждая щель давала минимум (sinj = m λ/ b), света не будет и при двух, и более щелях. Эти минимумы называются главными. Таким образом, условие главных минимумов можно записать в виде:
b sinj = m λ, где m = ±1, ±2, ±3…. (3)
Если оптическая разность хода волн, идущих от щелей (Δ = d sinj), равна целому числу длин волн, то волны интерферируют на максимум. Эти максимумы называются главными. Условие главного максимума можно записать в виде:
d sinj = m λ, где m = ±1, ±2, ±3…. (4)
Следует заметить, что число главных максимумов, находящихся между первыми главными минимумами, зависит от величины отношения d / b.
В направлениях, для которых выполняется условие
d sinj = m λ/2, (5)
где m = ±1, ±3, ±5 … наблюдаются минимумы интенсивности. Эти минимумы называются добавочными. Они возникают в результате интерференции волн, пришедших в точку Р от двух щелей. Добавочный минимум располагается между двумя главными максимумами.
Распределение интенсивности в дифракционной картине от двух щелей при d / b = 3 представлено на рис 5. Пунктирной кривой показано распределение интенсивности, при дифракции на одной щели.
Рис.5
Теорема Бабине.
Обычно теорема Бабине формулируется для случая фраунгоферовой дифракции. Эта теорема связывает дифракционные картины, наблюдаемые от дополнительных экранов в фокальной плоскости линзы.
Дополнительными экранами называются такие экраны, которые совместно перекрывают волновой фронт. Например, если в непрозрачной преграде имеется щель, то дополнительным к ней экраном является непрозрачная прямолинейная полоска, ширина которой равна ширине щели.
Согласно теореме Бабине, фраунгоферовы дифракционные картины от дополнительных экранов в фокальной плоскости линзы одинаковы везде, за исключением самого фокуса.
Доказать теорему можно, опираясь на принцип Гюйгенса-Френеля.
Если бы на пути параллельных лучей не было бы препятствия, то световое поле в фокальной плоскости линзы было бы всюду равно нулю, за исключением фокуса линзы.
Пусть вектор-амплитуда дифрагированной в некотором направлении волны для данного экрана равна Е 1, а для дополнительного к нему экрана в этом же направлении Е 2. В отсутствие обоих экранов амплитуды волн для всех направлений, кроме направления первоначальной волны, равны нулю. Следовательно, по принципу Гюйгенса – Френеля получим, что Е 1+ Е 2 = 0, откуда Е1 = Е2. Так как регистрируется интенсивность света I (I ~ Е2), то получаем, что I 1= I 2.
В данной работе экспериментально изучаются дифракционные фраунгоферовы картины от одной щели, двух щелей и тонкой нити.
Принадлежности: гелий-неоновый лазер, диафрагма с одной щелью, диафрагма с двумя щелями, диафрагма с тонкой нитью, экран.
Задание 1. Наблюдение и анализ дифракционной картины от одной щели.
Внешний вид экспериментальной установки показан на рис.6.
Рис.6
Свет от лазера (1) направляется на диафрагму (2) с вертикальной щелью, ширина которой может меняться с помощью микрометрического винта (3). Дифракционная картина наблюдается на экране (4), на котором закрепляется миллиметровая бумага.
1. Направьте пучок света от лазера вдоль оптической скамьи. Отметьте на экране положение светлого пятна. Эта точка будет являться центром дифракционной картины.
2. На оптической скамье установите диафрагму с одной щелью таким образом, чтобы плоскость щели была перпендикулярна оси лазерного пучка. На экране должна быть видна дифракционная картина, симметричная относительно отмеченной точки.
3. Микрометрическим винтом (3) установите такую ширину щели, при которой отчетливо видна дифракционная картина. Измерьте на экране расстояния Х 11, Х 22, Х 33 … (т.е. расстояния между первыми минимумами справа и слева от центрального максимума, вторыми и третьими, соответственно), расстояние от плоскости щели до экрана l (рис.7).
Рис.7
4. Вследствие малости углов, можно принять, что sinj» tgj. Записывая условие минимума (3) в виде: 
(здесь m = 1,2,3 …), получим: 
. Постройте график зависимости Хmm от m. Убедитесь в линейности этой зависимости и из ее наклона определите ширину щели b. Длина волны излучения гелий-неонового лазера λ=633 нм.
Задание 2. Наблюдение дифракционной картины от двух щелей и измерение расстояния между щелями.
Диафрагма с двумя щелями представляет собой раздвижную щель. Её ширину можно менять микрометрическим винтом. В середине щели натянута тонкая нить толщиной а. Эта нить разбивает щель на две равные щели с толщинами b.
1. Замените на оптической скамье диафрагму с одной щелью на диафрагму с двумя щелями. Установите плоскость щелей перпендикулярно к направлению лазерного пучка и перемещением щели в горизонтальном направлении, перпендикулярно оптической скамье, получите симметричную дифракционную картину.
2. Осторожно уменьшите ширину щели до размеров, когда дифракционная картина исчезнет.
3. Медленно увеличивайте ширину щели и внимательно следите за изменением характера дифракционной картины. Добейтесь, чтобы на экране получилась дифракционная картина, изображенная на рис.5 (между двумя первыми минимумами должно быть 5 максимумов). В этом случае d / b =3.
4. Измерьте углы дифракции, соответствующие главным минимумам, и вычислите ширину щели b из условия (3).
5. Зная, что a + b = d и d / b =3, вычислите расстояние между щелями а.
6. Изобразите примерную дифракционную картину при соотношении d / b =2. Получите на экране подобную дифракционную картину и вычислите расстояние между щелями а. Сравните результаты, полученные по разным дифракционным картинам.
Задание 3. Наблюдение дифракционной картины на дополнительных экранах.
В качестве дополнительных экранов используются одинарная щель и диафрагма с тонкой нитью.
1. На оптической скамье установите диафрагму с тонкой нитью, и получите на экране четкую дифракционную картину.
2. Измерьте расстояние X 33 и X 44 между третьими и четвертыми минимумами.
3. Вместо диафрагмы с нитью закрепите на оптической скамье щель и, меняя ее ширину, получите точно такую же дифракционную картину, которая наблюдалась от нити (чтобы расстояния X 33 и X 44 были бы такими же, как и в случае дифракции от нити).
4. Определите ширину щели методом, описанным в упражнении 1. Согласно теореме Бабине, толщина нити должна быть равна ширине щели.
5. Для сравнения определите толщину контрольного отрезка нити с помощью микрометра.
Контрольные вопросы
7. Явление дифракции света.
8. Принцип Гюйгенса–Френеля.
9. Классификация дифракционных явлений. Дифракция Френеля и Фраунгофера.
10. Дифракция Фраунгофера на одной и двух щелях.
11. Теорема Бабине.
12. Сформулируйте цель работы, опишите экспериментальную часть и обсудите результаты.
ЛАБОРАТОРНАЯ РАБОТА № 34
Изучение прозрачной дифракционной решетки
Цель работы: изучение дифракции Фраунгофера на одномерных периодических структурах.
Задача исследования:
1. Определение длин волн источника света (газоразрядной ртутной лампы) с помощью дифракционной решетки.
2. Определение дисперсии и разрешающей способности прозрачной дифракционной решетки.
Приборы и принадлежности: прозрачная дифракционная решетка, гониометр ГС-5 (прибор для точных измерений углов), газоразрядная ртутная лампа с источником питания.
Дифракционная решетка – это спектральный прибор, предназначенный для разложения света в спектр.
Под дифракционной решеткой понимается любая структура, обладающая пространственной периодичностью. Если свойства структуры периодически меняются в одном направлении, то решетка называется одномерной, если в нескольких направлениях – пространственной.
Дифракционные решетки бывают прозрачными и отражательными. Прозрачные решетки могут быть изготовлены путем нанесения с помощью алмазного резца параллельных штрихов на поверхность прозрачных пластинок. Промежутки между штрихами служат щелями. Отражательные решетки можно создать, нанося штрихи на поверхность отражающего покрытия.
Если дифракционная решетка изменяет только модуль амплитуды падающей световой волны, то такая дифракционная решетка называется амплитудной (например, система параллельных щелей). Если же дифракционная решетка модулирует фазу световой волны, то такая дифракционная решетка называется фазовой (например, решетки, у которых прозрачным штрихам придают определенный профиль).
Рассмотрим дифракцию Фраунгофера на амплитудной дифракционной решетке, представляющей собой систему одинаковых параллельных щелей, расположенных на равных расстояниях друг от друга.
Дифракционная картина является результатом многолучевой интерференции когерентных волн, исходящих от щелей решетки.
Рис. 1
Пусть плоская световая волна падает на дифракционную решетку ДР, содержащую N штрихов, нормально к ее поверхности (рис. 1). Лучи, дифрагированные под углом j, собираются в точке Р экрана Э, расположенного в фокальной плоскости линзы Л.
Расстояние между двумя соседними щелями равно d = a + b, где а - ширина непрозрачного промежутка, b – ширина щели. Величину d называют постоянной или периодом дифракционной решетки.
Если щели были бы не когерентными источниками, то в точке Р складывались бы интенсивности волн, пришедших от них. Поэтому дифракционная картина на экране представляла бы собой в N раз усиленную дифракционную картину от одной щели. Если же световые волны, испускаемее щелями когерентны, то в каждой точке наблюдения будет иметь место многолучевая интерференция, и дифракционная картина резко меняется.
Как и для одной щели, в направлении угла дифракции φ, определяемом условием:
b sinφ = m λ (m = ±1, ±2, ±3,...) (1)
ни одна щель не посылает света, и амплитуда результирующего колебания в соответствующей точке экрана равна нулю. Соотношение (1) определяет условие главных минимумов в дифракционной картине.
Для выяснения деталей дифракционной картины воспользуемся методом графического сложения амплитуд. Вектор результирующей амплитуды E 0 колебаний в точке Р представляет собой сумму векторов - амплитуд когерентных колебаний, приходящих в эту точку от каждой из N щелей: E 01, E 02 ,..., E 0N (рис.2). По модулю эти вектора одинаковы, и каждый следующий повернут относительно предыдущего на угол δ = (2π/λ)Δ, где Δ = d sinφ – оптическая разность хода. В зависимости от d на экране возникает то или иное значение результирующей амплитуды E 0.
Рис.2
Очевидно, что вектор E 0достигает максимальной длины, когда векторы E 0i расположены вдоль одной прямой.
Это имеет место при условии:
δ = 2π m или Δ = d sin φ = m λ, где m = 0, ±1, ±2, (2)
При этом длина вектора E 0 = N E 0i. Следовательно, интенсивность в света в точке Р будет достигать максимального значения: Imax = N2×Ii, где Ii – интенсивность, создаваемая в направлении j одной щелью. Условие (2) определяет положение главных максимумов в дифракционной картине.
Вектор E0 становится равным нулю каждый раз, когда ломаная линия, образованная векторами E 0i, обращается в замкнутую линию. Это будет происходить при значениях угла Nδ кратных 2π: Nδ = 2π m, т.е. когда δ = 2π m /N или:
d sinφ = m λ/N, m = ±1, ±2, …, m ¹ ±N, ±2N, …). (3)
Таким образом, при выполнении условия (3) волны, приходящие в точку Р от отдельных щелей, взаимно гасят друг друга. Условие (3) дает направления, по которым образуются добавочные минимумы. Интенсивность света в них равна нулю. Между двумя главными максимумами располагается N–1 добавочный минимум.
Положение главных максимумов зависит от длины волны. Поэтому при пропускании через дифракционную решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, коротковолновый конец которого обращен к центру дифракционной картины.
Способность дифракционной решетки разлагать свет в спектр позволяет использовать ее в качестве диспергирующего устройства в спектральных приборах.
Основными характеристиками дифракционной решетки, как спектрального прибора, являются дисперсия (угловая и линейная) и разрешающая способность.
Угловая дисперсия D определяется отношением углового расстояния δφ линий, отличающихся по длине волны на δλ, к величине этого интервала:
D = δφ/δλ (4)
Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие (2) главного максимума: d×cosφ×δφ = m δλ.
Отсюда:
. (5)
Линейная дисперсия Dлин определяется отношением линейного расстояния δ l на экране между спектральными линиями, отличающимися по длине волны на δλ, к величине этого интервала:
Dлин = δ l /δλ. (6)
Из рис.3 видно, что при небольших углах дифракции δ l ≈ f× δφ, где f - фокусное расстояние линзы, собирающей дифрагированные лучи на экране. Поэтому линейная дисперсия связана с угловой дисперсией соотношением:
Dлин = f×D (7)
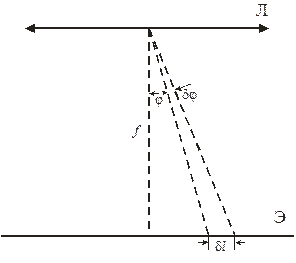
Рис.3
Разрешающей способностью спектрального прибора называется безразмерная величина R, равная:
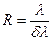, (8)
где δλ – наименьшая разность длин волн двух монохроматических спектральных линий, при которой спектральный прибор еще позволяет раздельно их наблюдать.
Разрешающая способность дифракционной решетки равна:
R = mN, (9)
где m - порядок спектра, N – число штрихов дифракционной решетки.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
В данной работе изучается плоская прозрачная дифракционная решетка. Перед выполнением практической части ознакомьтесь с описанием гониометра ГС-5 (оно приведено в работе «Изучение отражательной дифракционной решетки») и подготовьте его к измерениям. Внешний вид гониометра показан на рис.4.
Рис.4
ХОД РАБОТЫ
Поиск по сайту: