 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Изучение дифракции Френеля на круглом отверстии и полуплоскости
ЛАБОРАТОРНАЯ РАБОТА № 31
Цель работы: освоить методы наблюдения и анализа френелевских дифракционных картин от различных препятствий.
Если на пути сферической световой волны поместить небольшой непрозрачный экран с круглым отверстием на расстоянии a от точечного источника S, то на другом сплошном экране, расположенном на расстоянии b от отверстия, будет наблюдаться дифракционная картина в виде чередующихся темных и светлых концентрических колец (рис.1).
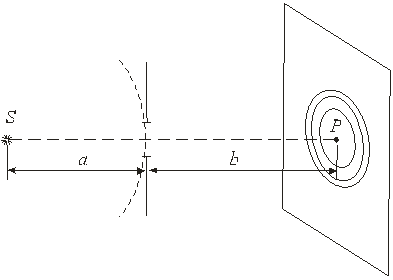
Рис.1
Для определения амплитуды (и соответствующей интенсивности) световой волны в точке Р экрана (точка Р находится на прямой, проходящей через источник S и середину отверстия), необходимо сложить амплитуды волн, приходящих от всех открытых зон Френеля, используя метод векторных диаграмм.
Радиус m -той зоны Френеля  Если радиус отверстия r0 окажется равным радиусу m -й зоны Френеля r m, то можно определить число зон Френеля m, открываемых данным отверстием:
Если радиус отверстия r0 окажется равным радиусу m -й зоны Френеля r m, то можно определить число зон Френеля m, открываемых данным отверстием:  . Видно, что число открытых зон Френеля зависит не только от r 0, но и от расстояний а и b. Меняя эти расстояния, можно изменять число зон, открываемых отверстием r 0. Если окажется, что Δ m = 1, то в центре дифракционной картины светлое пятно сменится на темное или наоборот, темное - на светлое.
. Видно, что число открытых зон Френеля зависит не только от r 0, но и от расстояний а и b. Меняя эти расстояния, можно изменять число зон, открываемых отверстием r 0. Если окажется, что Δ m = 1, то в центре дифракционной картины светлое пятно сменится на темное или наоборот, темное - на светлое.
Метод векторных диаграмм позволяет наглядно объяснить распределение интенсивности и при дифракции Френеля на полуплоскости и щели. Остановимся на анализе дифракционной картины от этих преград более подробно.
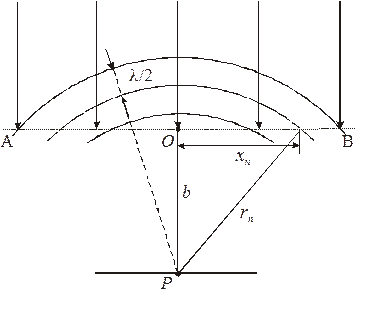 |
В этом случае волновой фронт целесообразно разбивать не на кольцевые зоны, как это делалось для круглых препятствий, а на полосатые зоны. Ограничимся случаем, когда волновой фронт плоский. Пусть плоскость волнового фронта АВ перпендикулярна плоскости чертежа (рис.2).
Рис.2
Расстояние от точки наблюдения Р до фронта АВ обозначим через b. Проведем цилиндрические коаксиальные поверхности, ось которых проходит через точку Р перпендикулярно плоскости рисунка, а радиусы увеличиваются на λ/2, т.е. равны b, b +λ/2, b +2λ/2,… Тогда волновой фронт АВ разобьется на прямоугольные полосы, которые называются зонами Шустера. Зоны Шустера отсчитываются вправо и влево от центральной точки О. Таким образом, центральная зона оказывается состоящей из двух зон. Из рис.2 видно:
 , (1)
, (1)
где rn и хn - расстояния от края n -й зоны до точки Р и точки О, соответственно. Аналогично для зоны с номером n -1 можно записать:  . Тогда
. Тогда
 (2)
(2)
Из этого соотношения следует:  . Отсюда легко могут быть найдены все
. Отсюда легко могут быть найдены все  . Т.к.
. Т.к.  0, то
0, то  ,
,  , …,
, …,  . Ширины зон Шустера Δ хn будут равны:
. Ширины зон Шустера Δ хn будут равны: 
 ,
,  ...
...  . Они монотонно убывают Δ х 1: Δ х 2: Δ х 3: Δ х 4... = 1: 0,41: 0,32: 0,27: ….
. Они монотонно убывают Δ х 1: Δ х 2: Δ х 3: Δ х 4... = 1: 0,41: 0,32: 0,27: ….
Для расчета результирующей амплитуды в точке Р, как и в случае зон Френеля, применим графический метод сложения амплитуд. Каждую зону Шустера разобьем на узкие полоски (подзоны) способом, аналогичным разбиению фронта на зоны Шустера, т.е. внося постоянную разность фаз для волн, идущих от соседних подзон. Колебания, возбуждаемые в точке наблюдения такими подзонами, на векторной диаграмме изобразятся векторами Δ A i, длина которых вначале резко убывает (вследствие значительного отличия площадей первых подзон), а затем становится почти одинаковой. Если перейти к пределу, устремив к нулю ширину каждой подзоны, то вместо ломаной получится плавная кривая, называемая спиралью Корню (рис.3).
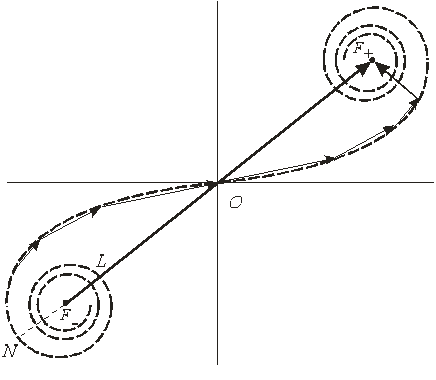
Рис.3
Она состоит из двух симметричных ветвей, обвивающихся вокруг фокусов F + и F -. Верхняя ветвь дает вклад в результирующую амплитуду вторичных волн, идущих от правой половины волнового фронта, а нижняя – от левой. При полностью открытом волновом фронте амплитуда световой волны в т. Р изображается вектором F - F +.
Рассмотрим теперь дифракционную картину на полуплоскости. Обозначим через a 0 = ׀ F - F +׀ и I 0 ~ a 02 амплитуду и интенсивность волны при полностью открытом волновом фронте, соответственно.
Когда точка Р находится на границе геометрической тени (координата х =0), для нее открыта только правая половина волнового фронта. Колебание в ней представится вектором OF + = 1/2 F - F +. Ему соответствует амплитуда  и интенсивность I 0/4 (рис 4).
и интенсивность I 0/4 (рис 4).
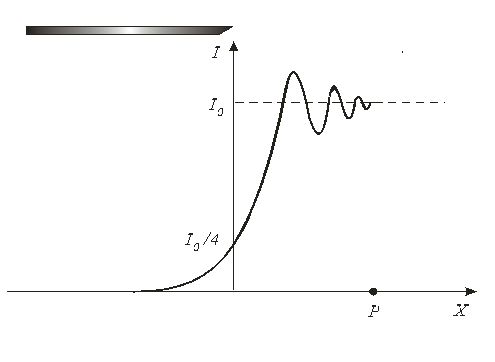
Рис.4.
При смещении точки Р в область геометрической тени полуплоскость станет закрывать все большее число зон правой половины волнового фронта. Поэтому начало результирующего вектора будет перемещаться по правой ветви, приближаясь к F +. В результате амплитуда и интенсивность колебания в точке Р будет монотонно стремиться к нулю.
Если точка Р смещается от границы геометрической тени вправо, в дополнение к правой части волнового фронта будет открываться все возрастающее число зон левой части фронта. При этом начало результирующего вектора амплитуды будет скользить по левой ветви спирали в направлении к F -. В результате амплитуда проходит через ряд максимумов (первый из них равен длине отрезка NF +) и минимумов (первый соответствует длине отрезка LF +) (рис.3). Зависимость интенсивности света I от расстояния x, показана на рис.4.
Поиск по сайту: