Ближняя и дальняя зоны дифракции

Дифракция возникает при любом локальном изменении волнового фронта, амплитудном или фазовом. Подобные изменения могут вызываться присутствием непрозрачных или частично прозрачных преград на пути волны (экранов), или участков среды с иным показателем преломления (фазовых пластинок). Характер дифракции зависит от значения безразмерного параметра (число зон Френеля укладывающихся в отверстии препятствия радиуса 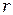). Из формулы (4.3) следует, что число зон при равно:

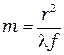(7.1)

где 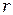- размер неоднородности, вызвавшей дифракцию, 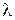- длина волны, и обозначено 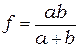- расстояние, по порядку величины равное расстоянию от неоднородности до точки наблюдения. Легко показать, что для плоской гармонической волны когда 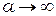, случай наиболее часто используемый на практике, 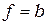, и формулу (7.1) можно переписать в виде:

(7.2)

Если параметр много меньше единицы, наблюдается дифракция Фраунгофера, если он порядка единицы — дифракция Френеля; наконец, если этот параметр много больше единицы, оказывается применимым приближение геометрической оптики. Для удобства сопоставления представим сказанное в следующем виде:

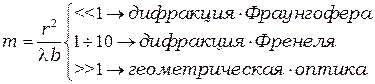(7.3)

Несмотря на то, что явление дифракции в оптике имеет место всегда, для наблюдения дифракции требуется постановка специальных экспериментов, в которых реализуется условие ~ 1 ÷ 10.

Рассмотрим теперь, как меняется интенсивность света 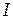на оси отверстия по мере увеличения расстояния от экрана с отверстием. Зафиксируем радиус отверстия 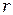. По мере удаления от отверстия число зон Френеля на отверстии уменьшается (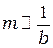), а интенсивность в центре экрана осциллирует: при нечётном числе открытых зон - увеличивается при чётном - уменьшается, пока наконец, в пределах отверстия не останется одна первая зона Френеля. В этот момент интенсивность света 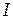в точке наблюдения достигает максимума (рис. 7.1), после чего монотонно убывает с ростом расстояния .

Расстояние между отверстием и экраном , при котором радиус первой зоной Френеля совпадает с радиусом отверстие 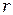, называют дифракционной длиной светового пучка или дистанцией Релея.

Из формулы (4.5) следует, что:

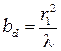(7.4)

Дифракционная длина определяет границу между двумя различными видами дифракции: дифракция в ближней зоне (или дифракция Френеля) и дифракция в дальней зоне (дифракция Фраунгофера) для заданного радиуса отверстия .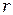

Дифракционная длина связана с числом зон Френеля. Из сравнения формулы (7.4) и формулы (4.5) видно, что

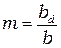. (7.5)

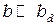
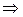
Отсюда и следует соотношения (7.3), когда 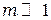, а когда .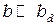

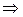
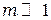Зона, для которой 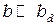, называется ближней зоной дифракции. В ближней зоне световой пучок сохраняет структуру, заданную формой отверстия, а интенсивность света на оси пучка примерноравна интенсивности исходной световой волны.

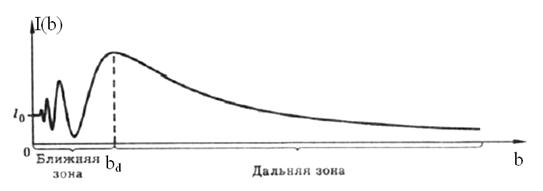
Рис. 7.1. Зависимость интенсивности света на оси отверстия от расстояния до экрана. - дифракционная длина светового пучка (дистанция Релея)

Для точек ближней зоны в пределах отверстия помещается множество зон Френеля, и поперечный профиль пучка поддерживается постоянным за счет интерференции элементарных вторичных волн, идущих от разных зон Френеля и его можно считать параллельным.

Зона, для которой 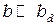называется дальней зоной дифракции. В этой зоне интенсивность света на оси пучка много меньше интенсивности исходной волны, и при больших значениях интенсивность слабо зависит от .

В дальней зоне световой пучок расширяется. Для точек дальней зоны в пределах отверстия помещается только центральная часть первой полуволновой зоны Френеля. Интерференция элементарных вторичных волн выражена слабее. Она уже не в состоянии поддерживать исходный поперечный профиль пучка, поэтому пучок становится расходящимся. Характер изменения поперечного размера светового пучка в процессе дифракции показан на рис. 7.2.

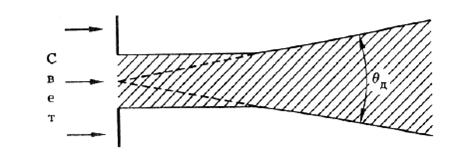
Рис. 7.2. Дифракция светового пучка и угол дифракционной расходимости .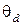

Оценим дифракционную Расходимость пучка 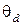(рис.7.3), исходя из представлений об интерференции элементарных вторичных волн. Полагая, что положение границы светового пучка определяется деструктивной интерференцией лучей, приходящих от противоположных границ отверстия, т.е. условием 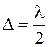, где 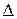— разность хода.

Рис. 7.3. К расчету дифракционной расходимости светового пучка.

Из рисунка видно, что 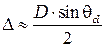, где 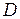- диаметр отверстия. Как правило, дифракционная расходимость невелика ( <<1), поэтому можно приближенно записать 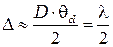, откуда следует, что

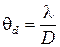. (7.6)

Таким образом, дифракционная расходимость светового пучка в дальней зонеопределяется отношением длины волны к начальному диаметру пучка 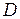: дифракционная расходимость пучка тем больше, чем меньше его начальный размер.Диаметр пучка в дальней зоне выражается формулой , — расстояние, отсчитываемое вдоль пучка от экрана с отверстием. Оценим дифракционную длину и угловую расходимость 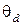для пучка гелий - неонового лазера: для 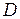= 2 мм, 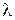= 0,6 мкм получим = 1,5 м, 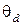= 3 10^-3 рад.

Из всего сказанного в этом разделе следует, что результат дифракции монохроматического излучения на каком-либо препятствии зависит не от абсолютных его размеров, а от числа перекрываемых им полуволновых зон.

При 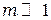(порядка нескольких сотен или тысяч открытых зон) дифракционные эффекты незначительны и распределение интенсивности приближенно описывается законами геометрический оптики (плоскость 1 на рис. 7.4).

Рис.7.4. Дифракционные распределения интенсивности света на различных
расстояниях от круглого отверстия.

Промежуточное условие (когда открыты единицы или десятки зон) соответствует дифракции Френеля и приводит к сложному распределению интенсивности, когда в центре картины может наблюдаться и минимум, и максимум (плоскости 2, 3 и 4 на рис. 7.4 и рис. 7.1 – ближняя зона).

При 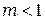перекрывается малая часть первой зоны и возникает важный для практики случай - дифракция Фраунгофера или дифракции в дальней зоне (плоскости 6 и 7 на рис. 7.4 и рис.7.2 – дальняя зона). Условной границей между двумя видами дифракции считают дистанцию Рэлея 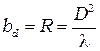, соответствующую расстоянию, на котором круглое отверстие диаметра 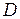, освещенное плоской монохроматической волной, открывает для центральной точки наблюдения одну первую зону ().

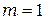Поиск по сайту: