Дифракция Фраунгофера

Если окажется, что расстояние от отверстия до точки наблюдения таково, что на отверстии укладывается менее одной зоны, то в точке Р будет всегда максимум, а вид дифракционной картины в плоскости экрана, перестает зависеть от величины . Из формулы (7.2) следует, что такой случай наблюдается, когда , т.е. когда

. (9.1)

В этом случае достаточно велико и можно считать, что лучи, идущие от крайних точек отверстия в точку M параллельны. Такая дифракция в "параллельных лучах" называется дифракцией Фраунгофера.

Таким образом, дифракция Фраунгофера наблюдается, когда источник света и точка наблюдения бесконечно удалены от препятствия вызывающего дифракцию. Фронт волны на препятствии при дифракции Фраунгофера представляет собой плоскость.

На примере дифракции на кольце (рис.9.1) можно проследить плавный переход от геометрической оптики (1-3) через дифракцию Френеля (4-7) к дифракции Фраунгофера (9-11).

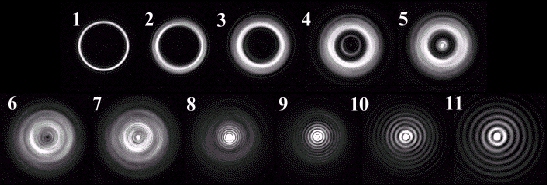
Рис. 9.1. Границы дифракционных приближений. Дифракция на кольце. Число открытых зон уменьшается слева направо, при этом значение 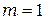(дистанция Рэлея, условная граница между дифракциями Френеля и Фраунгофера) соответствует снимку 8.

Поиск по сайту: