ГЛАВА 7. Дифракция пЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ИДЕАЛЬНО ПРОВОДЯЩЕМ ЦИЛИНДРЕ

7.1 Дифракция плоской электромагнитной волны на идеально проводящем цилиндре

Рассмотрим задачу о дифракции плоской волны на идеально проводящем цилиндре радиусом 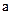, ось которого ориентирована вдоль оси декартовой системы координат (рис.7.1). Считается, что данный цилиндр, выполненный из идеального проводника (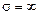) и бесконечно протяжен в осевом направлении. Плоская электромагнитная волна с линейной поляризацией падает на цилиндр слева направо в положительном направлении оси , как показано на рисунке 7.1. Плоскость поляризации падающей волны выбрана таким образом, что соответствующий вектор напряженности электрического поля имеет единственную отличную от нуля проекцию 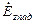, которая считается известной. Требуется вычислить пространственное распределение комплексной амплитуды электрического вектора дифрагированной волны во всем пространстве.

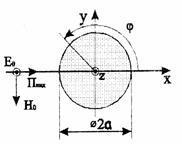
Рис. 7.1 - Падение плоской электромагнитной волны на идеально проводящий цилиндр

Для этого введем цилиндрическую систему координат 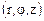и запишем комплексную амплитуду вектора напряженности электрического поля падающей волны в следующем виде:

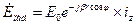. (7.1)

Проекция этого вектора на ось является периодической функцией угловой координаты 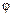с периодом 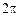, поэтому можно воспользоваться разложением в ряд Фурье; коэффициентами такого ряда служат функции Бесселя 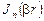. В результате будем иметь:

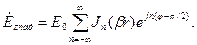(7.2)

Очевидно, что при выбранной поляризации поле рассеянной волны будет иметь единственную отличную от нуля проекцию 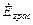вектора напряженности электрического поля. При этом на поверхности идеально проводящего цилиндра должно выполняться очевидное граничное условие

(7.3)

Рассеянное поле должно являться решением однородного уравнения Гельмгольца 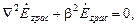которое в данном случае приобретает вид

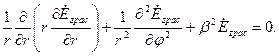(7.4)

Рассеянное поле существует в бесконечной области , причем при 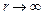должно выполняться условие излучения Зоммерфельда. Решение уравнения (7.4) представляет собой периодическую функцию аргумента 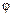с периодом 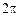, которую можно искать в виде ряда Фурье, совпадающего по форме с (7.2)

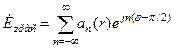(7.5)

с не известными амплитудными коэффициентами 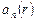отдельных угловых гармоник. Поскольку 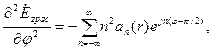каждый из этих коэффициентов должен быть решением дифференциального уравнения второго порядка 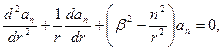которое заменой переменной 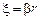сводится к обычному уравнению Бесселя

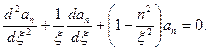(7.6)

Подходящей системой линейно независимых решений уравнения (7.6) служат функции Ганкеля и 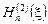первого и второго рода соответственно. При больших значениях аргумента справедливы следующие асимптотические формулы:

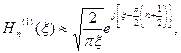
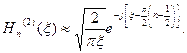
Ясно, что цилиндрическую волну, уходящую на бесконечность, описывает функция 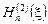. Таким образом,

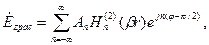(7.7)

причем в соответствии с (7.2) для выполнения граничного условия на поверхности цилиндра необходимо потребовать, чтобы

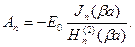(7.8)

Итак, комплексная амплитуда электрического вектора рассеянного поля выражается бесконечным рядом Фурье

(7.9)

На большом удалении от цилиндра (при 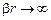) это поле имеет вид цилиндрической волны с неоднородным угловым распределением амплитуды:

(7.10)

Полученный ряд быстро сходится только при 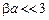; расчет дифракционного поля в случае цилиндров достаточно большого радиуса представляет определенные трудности.

Поиск по сайту: