Понятие «лучевой трубки»

Анализ показывает, что для ближней зоны характерна локализация энергии электромагнитного поля в пределах «лучевой трубки», поперечник которого сравним с размерами апертуры (рис. 5.4).

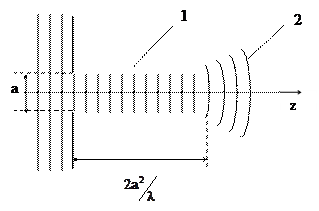Рис. 5.4 – Характер распределения поля в ближней зоне апертурной антенны:

1 – лучевая трубка; 2 – сферическая волна

Чтобы вычислить дифракционное поле в ближней зоне воспользуемся для следующим выражением:

. (5.15)

Волновая картина, рассматриваемая в данном приближении, соответствует дифракции Френеля.

Будем рассматривать случай, когда поле вблизи излучающей оси излучающей системы . Подставив (5.15) в (5.8) получим

. (5.16)

Зависимость поля от координат и в формуле (5.16) выражается как произведение интегралов одинаковой структуры. Рассмотрим один из них:

.

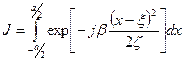Используя подстановку

,

получим

.

Такие интегралы принято выражать через неэлементарные функции – интегралы Френеля

,

,

так что

.

Воспользовавшись последним равенством, получим

, (5.17)

где введен параметр .

Обычно используется не сама величина 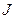, а квадрат ее модуля , который пропорционален среднему значению вектора Пойтинга. При дифракции Френеля сохраняются многие черты чисто лучевой оптики. Значения и служат условными границами областей света и тени. Интенсивность поля в освещенной области оказывается немонотонной функцией пространственных координат (рис.5.5).

Рис. 5.5 - Характер распределения интенсивности поля вблизи границы между освещенной областью (1) и областью тени (2)

ГЛАВА 6. Метод геометрической оптики

Поиск по сайту: