 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Условие излучения
Предположим, что точечный источник гармонических электромагнитных волн помещен в начало сферической системы координат. Среда распространения имеет следующие характеристики:
Обозначим через 
комплексную скалярную функцию, представляющую собой комплексную амплитуду произвольно взятой проекции одного из векторов электромагнитного поля. Всюду, за исключением точки 
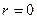, функция удовлетворяет однородному уравнению Гельмгольца:
(1.1)
где 
- коэффициент фазы волнового процесса при заданной частоте излучения источника.
Для простоты считаем, что обладает сферической симметрией, т.е. она не зависит от угловых координат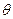 
и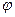 
. Используя выражение оператора Лапласа в сферической системе координат, получим:
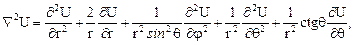
(1.2)
Применив непосредственную подстановку, легко проверить, что уравнение (1.2) эквивалентно уравнению
(1.3)
которое не содержит первой производной. Равенство (1.3) представляет собой классическое уравнение гармонического осциллятора. Система его решений состоит из двух функций, вида 
.
Полагая, что соответствующие амплитудные коэффициенты равны единице, находим два линейно-независимых решения уравнения (1.2)
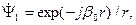(1.4)
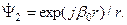(1.5)
Разные знаки аргументов экспоненциальных функций означают, что первому решению соответствует сферическая волна, уходящая от источника на бесконечность.
Второе решение описывает аналогичную сферическую волну с противоположным направлением распространения, т.е. волну, которая приходит из бесконечности в точку размещения источника.
Из повседневного опыта известно, что волны, возбужденные источником и ушедшие в свободное пространство никогда не возвращаются назад. Поэтому решение вида (1.5) исключается из рассмотрения. Для анализа полученных решений сложных дифракционных задач требуется аналитический критерий, который позволил бы отличить волны, уходящие на бесконечность от физически нереализуемых волновых процессов, приходящих из бесконечности к источнику.
Этот критерий был найден в начале ХХ века немецким физиком А.Зоммерфельдом, который показал, что любое решение уравнения Гельмгольца, обладающее свойством волны, уходящей на бесконечность, должно при 
удовлетворять предельному условию вида:
. (1.6)
В теории волновых процессов формулу (1.6) называют условием излучения или условием Зоммерфельда.
Поиск по сайту: