 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формула Кирхгофа
В середине XIX века немецкий физик Г.Кирхгоф (1984 – 1887 гг.) доказал, что решение поставленной задачи дается формулой:
, (4.1)
где 
– расстояние между текущей точкой поверхности и точкой наблюдения 
. Доказательство формулы Кирхгофа основывается на известной из курса математики теореме Грина, согласно которой дважды дифференцируемые функции 
и 
пространственных координат, удовлетворяют тождеству:
. (4.2)
Предположим, что как искомая функция , так и вспомогательная функция в области 
являются решениями одного и того же уравнения Гельмгольца
(4.3)
Очевидно, что в силу уравнений (4.3) левая часть формулы (4.2) обращается в нуль
. (4.4)
Будем считать, что вспомогательной функцией служит уже известное решение скалярного уравнения Гельмгольца
, (4.5)
описывающее расходящуюся сферическую волну. Здесь под 
подразумевается длина отрезка между выбранной точкой наблюдения 
и произвольной точкой внутри объема 
.
Поскольку функция в точке имеет особенность, исключим из области малый шар радиусом 
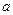с центром в точке . Обозначив символом 
поверхность этого шара, на основании (4.4) можно записать
(4.6)
Следующим этапом вычислим подынтегральное выражение в левой части формулы (4.6), так как перемещение по направлению нормали к поверхности означает увеличение координаты , то
. (4.7)
Поэтому левую часть равенства (4.6) можно представить в виде
. (4.8)
Теперь устремим к нулю радиус вспомогательной сферы, учитывая, что искомое поле , по предположению, внутри не имеет источников и поэтому всюду ограничено и непрерывно. В подынтегральное выражение (4.8) входят слагаемые, обратно пропорциональные как первой степени, так и квадрату текущего радиуса. Легко проверить, что вклад слагаемых первой степени равен нулю:
, (4.9)
поскольку площадь сферы, равная 
, стремится к нулю быстрее, нежели ее радиус. В то же время
. (4.10)
На основании изложенного из равенства (4.6) получаем выражение для расчета искомого поля в точке
,
совпадающее с формулой Кирхгофа (4.1).
ГЛАВА 5. ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ПРЯМОУГОЛЬНОМ ОТВЕРСТИИ В ИДЕАЛЬНО ПРОВОДЯЩЕМ ЭКРАНЕ
Поиск по сайту: